This post is about SVD for investment analysis.
What is Singular Value Decomposition
For a set of orthogonal vectors, after a linear transformation, their magnitudes may change, but they can still remain orthogonal. What is this orthogonal set, and what is the result after the linear transformation?
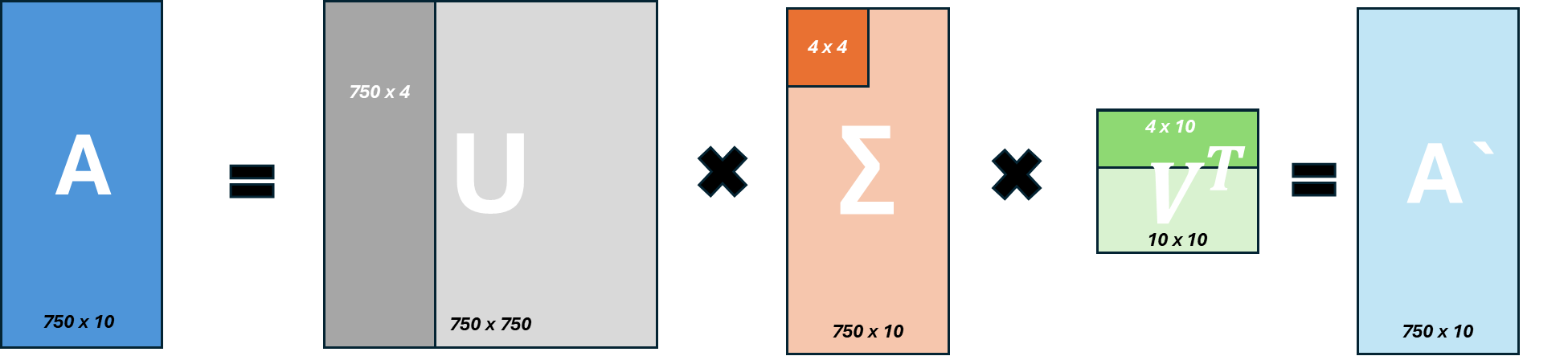
SVD is decompose matrix A which can be decomposed into $ \text{U} \times \Sigma \times V^{T}$. In here each matrixs have below size and characteristics.
A: $(m \times n)$ rectangular matrix
U: $(m \times m)$ orthogonal matrix (User matrix)
$\Sigma$: $(m \times n)$ diagonal matrix (Singular Values $\lambda$ in Matrix)
V: $(n \times n)$ orthogonal matrix (Singular Vector)
In terms of linear transformation SVD can be described as follows. In here, orthogonal matrix(U) is a matrix $ UU^T = I $ and thus $U^T = U^{-1}$
$ AV = U \Sigma $
$ AVV^{-1} = U \Sigma V^{-1}$
$ AVV^{T} = U \Sigma V^{T} $
$ A = U \Sigma V^{T}$
Eigenvector exists if the matrix A is square matrix, while singular vector can be defined for both square and rectangular matrix. In fact, for symmetric matrices, the eigenvectors and the singular vectors are the same, and the eigenvalues correspond to the singular values. However, for non-symmetric or rectangular matrices, this relationship does not hold.
The orthogonal vectors ( $\vec{x}$, $\vec{y}$ ), shown in the example before the linear transformation, can be thought of as a collection of column vectors, which corresponds to the ( V ) matrix in ( $A = U \Sigma V^{T} $).
$ V = \begin{pmatrix} \vec{x} \vec{y} \end{pmatrix} \tag{8} $
Additionally, the orthogonal vectors after the linear transformation, $( A \vec{x}, A \vec{y} )$, can be normalized to have unit length as $(\vec{u}_1, \vec{u}_2)$. The collection of these column vectors corresponds to the ( U ) matrix in $( A = U \Sigma V^T )$.
$ U = \begin{pmatrix} \vec{u}_1 & \vec{u}_2 \end{pmatrix} \tag{9} $
Finally, the singular values (i.e., scaling factors) can be gathered into the $ ( \Sigma ) $ matrix as shown below. In dimensionality reduction stage level of variance explained can be calculated by how many singluar values you choose in this matrix. $ \Sigma = \begin{bmatrix} \sigma_1 & 0
0 & \sigma_2 \end{bmatrix} \tag{10} $
If you choose only $ \sigma_1 $ in dimensionality reduction, variance explained in dimensionality reduction can be expressed as follows:
Var Explained = $\frac{\sigma_1}{\sigma_1 + \sigma_2} $
Combining this explained variance in singular values, $V^{T}$, can be used to explain the portfolio. Here we suppose that we have a portfolio with $N$ assets, and each asset has an equal weight $\frac{1}{N}$. If we use only $\sigma_1$ for dimensionality reduction, the portfolio with weights $\vec{u}_1 \times \text{original weight}$ = $\vec{u}_1 \cdot \left(\frac{1}{10}, \frac{1}{10}, \ldots , \frac{1}{10}\right)$ explains $\frac{\sigma_1}{\sigma_1 + \sigma_2}$ of the variance of the original portfolio.
In here, matrix V is called singular matrix which consists of n singular vectors (Eigenvector). The left singular vectors U come from the rows of A, and the right singular vectors V come from the columns of A. This means that The left singular vectors U correspond to the domain (input) of the transformation, while the right singular vectors V correspond to the codomain (output).
How this can be used in investment portfolio
For our application in investment portfolio, which consists of time series data, formulation of SVD will follow below. We are going to use three years ETF return data ($ 250 \times 3 = 750$). And there are 10 ETFs in our portfolio. So, matrix A will have $(750 \times 5)$. Graphically, it would be like this.
The power of Singular Value Decomposition (SVD) shines in the process of reconstructing a decomposed matrix.
Using only ( p ) singular values, we can approximate the matrix ( A’ ) from the original matrix ( A ), which was decomposed into ( U, $\Sigma$, $V^{T}$ ). As mentioned earlier, since the amount of information in ( A ) is determined by the magnitude of the singular values, even with only a few large singular values, we can retain a significant amount of useful information. $A \approx {U_p} \Sigma_p {V_p}^T$
Application in Portfolio
Let’s use this idea in investment portfolio. First, We are going to use 10 major US sector ETFs and compared with S&P500.
1
2
3
4
5
6
7
8
9
10
The Technology Select Sector SPDR Fund (XLK)
The Communication Services Select Sector SPDR ETF Fund (XLC)
The Health Care Select Sector SPDR Fund (XLV)
The Energy Select Sector SPDR Fund (XLE)
The Consumer Discretionary Select Sector SPDR Fund (XLY)
The Industrial Select Sector SPDR Fund (XLI)
The Materials Select Sector SPDR Fund (XLB)
The Financial Select Sector SPDR Fund (XLF)
The Utilities Select Sector SPDR Fund (XLU)
The Consumer Staples Select Sector SPDR Fund (XLP)
For Multi Asset Perspective, we selected following major asset class ETFs and compared with Moderate Asset Allocation from Blackrock (AOM).
1
2
3
4
5
6
7
8
9
10
11
12
SPDR Dow Jones Industrial Average ETF Trust (DIA)
SPDR S&P 500 ETF Trust (SPY)
Invesco QQQ Trust (QQQ)
iShares Core MSCI International Developed Markets ETF (IDEV)
iShares Core MSCI Emerging Markets ETF (IEMG)
iShares Core U.S. Aggregate Bond ETF (AGG)
iShares 20+ Year Treasury Bond ETF (TLT)
iShares 1-3 Year Treasury Bond ETF (SHY)
iShares iBoxx $ Investment Grade Corporate Bond ETF (LQD)
iShares Core International Aggregate Bond ETF (IAGG)
SPDR Gold Shares (GLD)
Vanguard Real Estate Index Fund ETF Shares (VNQ)
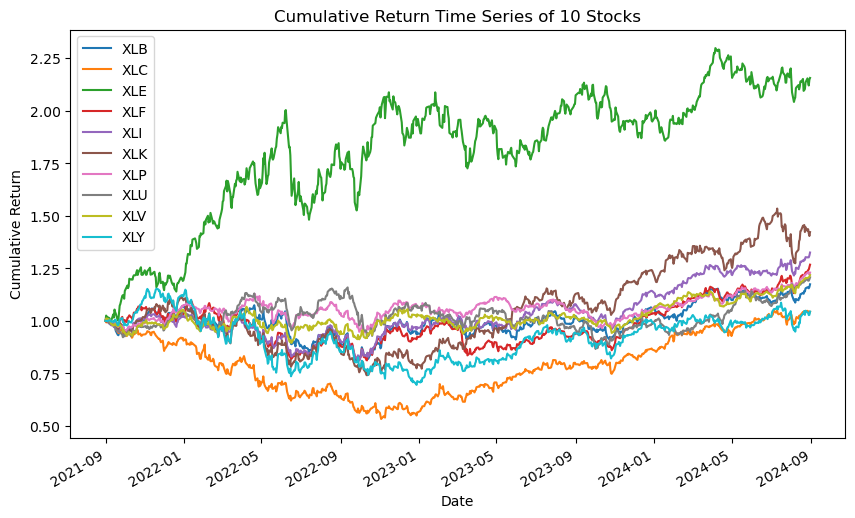
Below figure shows the cumulative returns of 10 major US sector ETFs and compared with S&P500.
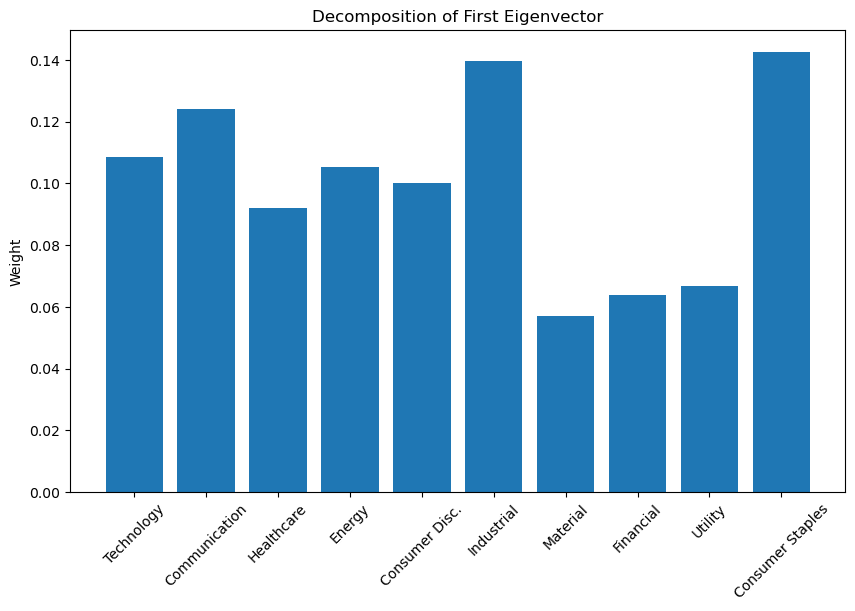
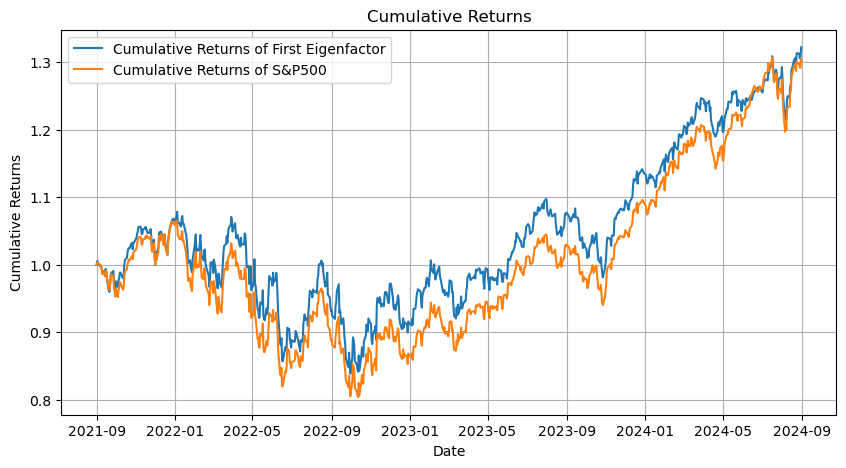
After eigenvalue decomposition, I came up with first eigenvector, which are like below.
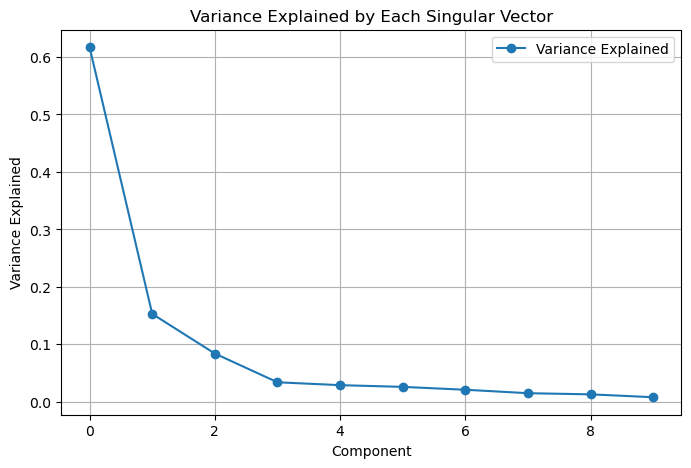
Below graph shows how eigenvector explains the variance. And we decided to use the first eigenvector which explains around 60% of total variance.
Lastly, portfolio constructed with first eigenvector efficiently track the benchmark with limited number of equities while maintain adequate performance
Full Code
Full code can be fond below link. CODE
Let’s code this idea
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
import os
import sys
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import yfinance as yf
from numpy import linalg as LA
# Define the tickers
tickers = ['XLK','XLC','XLV','XLE','XLY','XLI','XLB','XLF','XLU','XLP']
labels = ['Technology', 'Communication', 'Healthcare', 'Energy', 'Consumer Disc.', 'Industrial', 'Material', 'Financial', 'Utility', 'Consumer Staples']
# Fetch historical data
def fetch_data(tickers, start_date, end_date):
data = yf.download(tickers, start=start_date, end=end_date)['Adj Close']
return data
# Collect data
data = fetch_data(tickers, '2021-09-01', '2024-09-01')
spy = fetch_data(['SPY'], '2021-09-01', '2024-09-01')
# Drop rows with missing data
data = data.dropna()
spy = spy.dropna()
# Calculate daily returns
returns = data.pct_change().fillna(0)
spy_returns = spy.pct_change().fillna(0)
cum_returns = (1 + returns).cumprod()
df_cum_returns = (1+returns).cumprod()
# Normalize the data
# returns_normalized = (returns - returns.mean()) / returns.std()
# spy_returns_normalized = (spy_returns-spy_returns.mean()) / spy_returns.std()
# Perform SVD using numpy.linalg
U, S, VT = LA.svd(returns)
# Print results
print("Singular values:", S)
print("VT (transposed):", VT.T)
# Compute variance explained by each singular vector
var_explained = np.round(S**2 / np.sum(S**2), decimals=3)
print('Variance explained by each singular vector:', var_explained)
print("First Eigenfactor VT[0] = ", VT[0])
weight_factor_1 = abs(VT[0]) / sum(abs(VT[0]))
print("First Eigen portfolio weight = "weight_factor_1)
# Choose First Eigenfactor
weighted_returns = returns.mul(weight_factor_1, axis=1)
scaled_weighted_returns = weighted_returns.div(np.sqrt(S[0]))
cumulative_returns = (1 + scaled_weighted_returns.sum(axis=1)).cumprod()
spy_cumulative_returns = (1 + spy_returns).cumprod()
# Calculate cumulative returns for each stock
cumulative_returns_stocks = (1 + returns).cumprod()
# Ensure the cumulative returns of the eigenfactor is aligned in terms of dates with original data
cumulative_returns_aligned = cumulative_returns.loc[returns.index]
# Compute the correlation of each stock's cumulative returns with the eigenfactor cumulative returns
correlations = cumulative_returns_stocks.corrwith(cumulative_returns_aligned)
# Print the correlation results
print("Correlation of each stock's cumulative returns with the cumulative returns of the first eigenfactor:")
print(correlations)
Conclusion
In this project, the first singular vector of the returns of the major stock sector ETFs was used to identify the key drivers of the S&P500 market index returns. Even though the variance of the returns explained by the first singular vector is only 62%, the first singular vector still accounts for the most variance among the singular vectors and is significant for understanding the returns. By comparing the magnitude of the coefficients in the first singular vector, I chose the top 10 most dominant drivers to be the key drivers that were used to create small portfolios. Via data analysis, I created portfolio structures which efficiently track the benchmark with limited number of equities while maintain adequate performance. Even though this project used simplified models with only five years of data and is impractical to be directly used for investment, after applying further analyses building on this project to different benchmarks and various pools of assets, there is a potential to ease the difficulty of managing large portfolios and provide a solution to the problem of high transaction costs and fees.