This post is about credit default swap. Though CDS is not familiar, CDS can be used to protect from credit risk and market risk. If you heavily invest on foreign currency based bond for long term, and the bond has default risk, CDS is absoultely what you are looking for.
What is Market risk
Market risk includes risk derived from interest rate, foreign currency exchnage rate fluctuation. These factors are mainly discussed in macro ecnoomy market. Forward Rate Agreement, Interest Rate Swap, and Cross Currency Swap are examples of financial instruments intened to protect from macro economic variable.
Whart is Credit risk
If you just invest in US treasury or treasury of soverign country and wriiten in local currency, you don’t have to deal with credit risk. But, if you want to invest in corporate bond or sovereign bond of emerging country, you need to worry about default risk. CDS is the instrument to mitigate credit risk when default happens.
What is Credit Default Swap
CDS is an insurance contract, which you can receice payment when default happens. Suppose you are portfolio manager at Korea, you want to invest emerging bond in US with USDollar. What you need to worry about is default of company or country and fluctuation of interest rate. Supoose you are investing on corporate bond in US, you need to worry about default of company too. Before CDS there was no adequate method to mitigate credit risk only, since corporate bond rate is sum of market risk and credit risk.
Cashflow of CDS seller, who receive premium for giving protection to buyer, is like below. He/She receive fixed CDS premium at interest payement date. If default does not happens, CDS seller just receive premiums only. If default happens, CDS seller pays notional amount and receive impaired underlying asset. Since impaired asset, which is usually corporate bond, can recover after default, we need to consider recovery rate. However, this number vary by industry and it is determined by accountants and lawyers. So, in here we set recovery rate to zero.
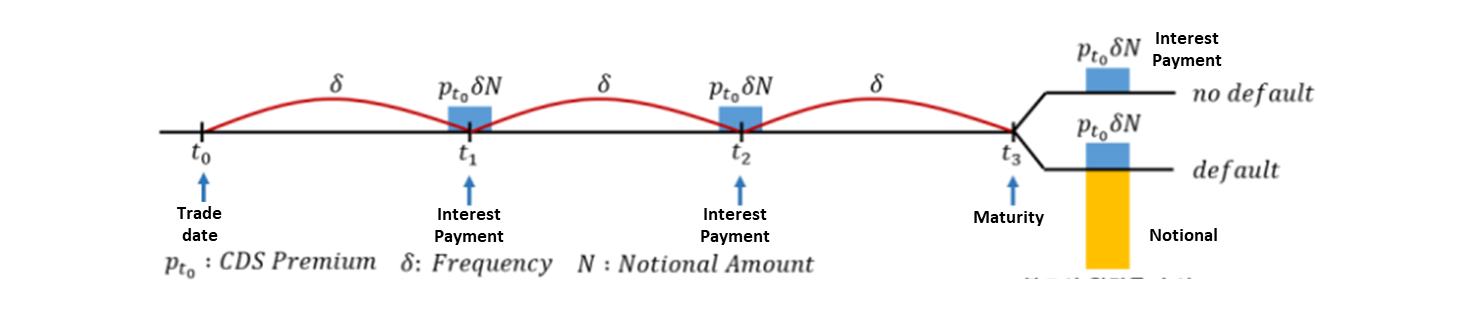
From corporate bond to CDS
Below picture shows typical cashflow from corporate bond.
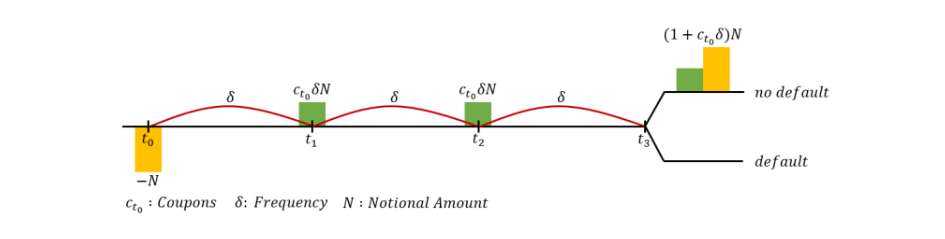
Cashflow of corporate bond can be decomposed into interest, principal and payment at default.
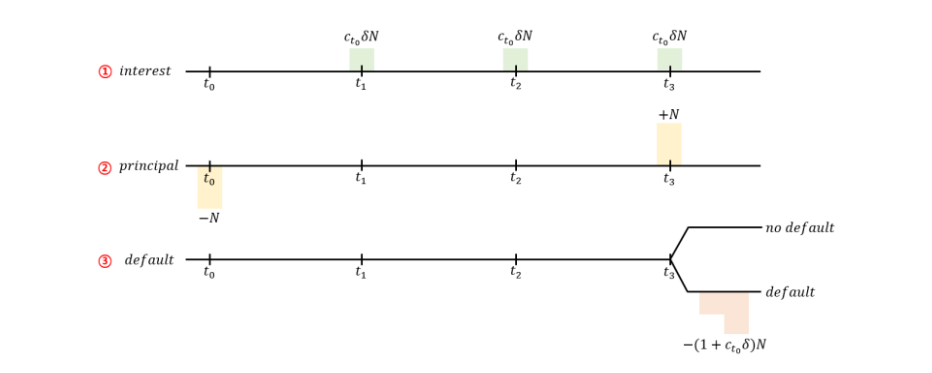
We divide interest part to market risk and credit risk. And “asset swap spread” can be declared like this. $ Asset Swap Spread = CorporateBondYield - SwapSpread $. Using this, corporate bond interest can be decomposed like this.

Now, we change interest part and principal part into Interest Rate Swap and Floating rate bond investmebt.

In here, we add Asset Swap Spread(represent credit risk of corporate bond) to default part like below.
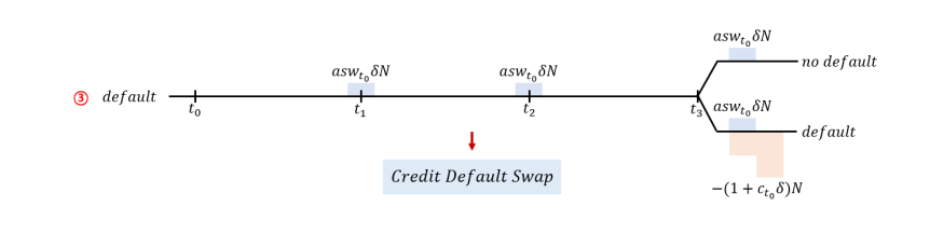
Buyer and seller of credit default swap (CDS)
Bid CDS (Protection Buy) = Sell corporate bond + Receive Interest Rate Swap + Buy Floating Rate Note
Ask CDS (Protection Sell) = Buy corporate bond + Pay Interest Rate Swap + Buy Floating Rate Note
Summary
See below picture, if you are facing trouble in memorizing the CDS structure. 
Prequisite
You need two curve to price CDS. Since it is long-term contract with underlying asset of bond, discount curve is needed. In here, swap_curve function is to discount future cash flow. In addition, you need to calculate harzard rate since it has possibility of default. In here, cds_curve function is to discount expected cashflow at maturity considering default probability.
1
from quant_lib.cds_curve import get_irs_quote, get_cds_quote, swap_curve, cds_curve
If you don’t want to make your own swap curve library, go to this link and download and place it appripriate directory. CDS_Curve_Code
Data for this project can be found here.
CDS_Data
Result
Let’s price credit default swap
1
2
3
4
price of CDS = 964810.2233
IR Delta = -236.2413
Credit Delta = -2693.3063
Theta = 75.4122
Let’s code this idea
Full code can be found at below link.
CODE
Full Code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
import os
import datetime
import numpy as np
import pandas as pd
import QuantLib as ql
from quant_lib.cds_curve import get_irs_quote, get_cds_quote, swap_curve, cds_curve
class CDS():
def __init__(self, today, maturity_date, spread, recovery, notional, position):
# initial setup
self.date = today
self.discount_curve_t0 = self.discount_curve(self.date)
self.cds_curve_t0 = self.cds_curve(self.date)
self.maturity_date = ql.Date(maturity_date.day, maturity_date.month, maturity_date.year)
if position == 'long':
self.position = ql.Protection.Buyer
else:
self.position = ql.Protection.Seller
self.spread = spread
self.notional = notional
self.recovery_rate = recovery
self.tenor = ql.Period(3, ql.Months)
self.calendar = ql.UnitedStates()
self.convention = ql.ModifiedFollowing
self.dateGeneration = ql.DateGeneration.CDS
self.dayCount = ql.Actual360()
self.endOfMonth = False
# pricing result
self.npv = self.pricing(self.discount_curve_t0, self.cds_curve_t0)
self.ir_delta = self.ir_delta()
self.credit_delta = self.credit_delta()
self.theta = self.theta()
def discount_curve(self, date):
return swap_curve(date, get_irs_quote(date))
def cds_curve(self, date):
return cds_curve(date, get_cds_quote(date), swap_curve(date, get_irs_quote(date)))
def pricing(self, discount_curve, cds_curve):
# processing
todays_date = ql.Date(self.date.day, self.date.month, self.date.year)
discount_curve_handle = ql.YieldTermStructureHandle(discount_curve)
schedule = ql.Schedule(todays_date,
self.maturity_date,
self.tenor,
self.calendar,
self.convention,
self.convention,
self.dateGeneration,
self.endOfMonth
)
cds = ql.CreditDefaultSwap(self.position,
self.notional,
self.spread/1000,
schedule,
self.convention,
self.dayCount
)
probability = ql.DefaultProbabilityTermStructureHandle(cds_curve)
engine = ql.MidPointCdsEngine(probability=probability,
recoveryRate=self.recovery_rate,
discountCurve=discount_curve_handle
)
cds.setPricingEngine(engine)
npv = cds.NPV()
return npv
def ir_delta(self):
curve_handle = ql.YieldTermStructureHandle(self.discount_curve_t0)
# 1bp
basis_point = 0.0001
# CDS price when 1bp up
up_curve = ql.ZeroSpreadedTermStructure(curve_handle, ql.QuoteHandle(ql.SimpleQuote(basis_point)))
up_cds = self.pricing(up_curve, self.cds_curve_t0)
# CDS price when 1bp down
down_curve = ql.ZeroSpreadedTermStructure(curve_handle, ql.QuoteHandle(ql.SimpleQuote(-basis_point)))
down_cds = self.pricing(down_curve, self.cds_curve_t0)
# interest rate delta
return (up_cds - down_cds) / 2
def credit_delta(self):
_cds_quote = get_cds_quote(self.date)
# CDS price when 1bp up
_cds_quote['Market.Mid'] += 1
up_curve = cds_curve(self.date, _cds_quote, self.discount_curve_t0)
up_cds = self.pricing(self.discount_curve_t0, up_curve)
# CDS price when 1bp down
_cds_quote['Market.Mid'] -= 1
down_curve = cds_curve(self.date, _cds_quote, self.discount_curve_t0)
down_cds = self.pricing(self.discount_curve_t0, down_curve)
# credit delta
return (up_cds - down_cds) / 2
def theta(self):
price_t0 = self.pricing(self.discount_curve_t0, self.cds_curve_t0)
discount_curve_t1 = self.discount_curve(self.date + datetime.timedelta(days=1))
cds_curve_t1 = self.cds_curve(self.date + datetime.timedelta(days=1))
price_t1 = self.pricing(discount_curve=discount_curve_t1, cds_curve=cds_curve_t1)
theta = price_t1 - price_t0
return theta
## build CDS contract information
todays_date = datetime.date(2020, 12, 11)
maturity_date = datetime.date(2025, 12, 11)
notional = 10000000
spread = 20.5241
recovery = 0.4
position = 'short'
# build CDS object
cds = CDS(
today=todays_date,
maturity_date=maturity_date,
spread=spread,
recovery=0.4,
notional=notional,
position=position
)
# Print result
print("price of CDS = {}".format(round(cds.npv,4)))
print("IR Delta = {}".format(round(cds.ir_delta,4)))
print("Credit Delta = {}".format(round(cds.credit_delta,4)))
print("Theta = {}".format(round(cds.theta,4)))