This post is about interest rate swap. Though IRS is not familiar, IRS can offer interest rate risk mitigation or chance to seize from interest rate fluctuation.
What is Interest Rate Swap
Interest rate swap is method to mitigate interest rate risk. If you buy IRS, you can pay fixed swap rate until maturity, while you receive floating rate(such as LIBOR) to counterparty.
Since, size of this contract is huge, it is mainly field of institutional players. I strongly recommend you to study this material for your future goal, becomming rich enough to trade IRS with your own capital. IRS combined with FX market makes huge impacts. Big IRS contracts sometimes impacts FX market. Suppose you are foreign bond investors (at dollar perspective), you might want to secure fixed income at your currency, then you might go to Forward market. So interest rate (bond) and fixed income is inevitable.
Buyer of interest rate swap(IRS)
Suppose you are investor of floating bond investors, you might worry about fluctuating interest rate. To mitigate this, you buy IRS. So, you receive floating interest rate and pay fixed rate(swap rate). 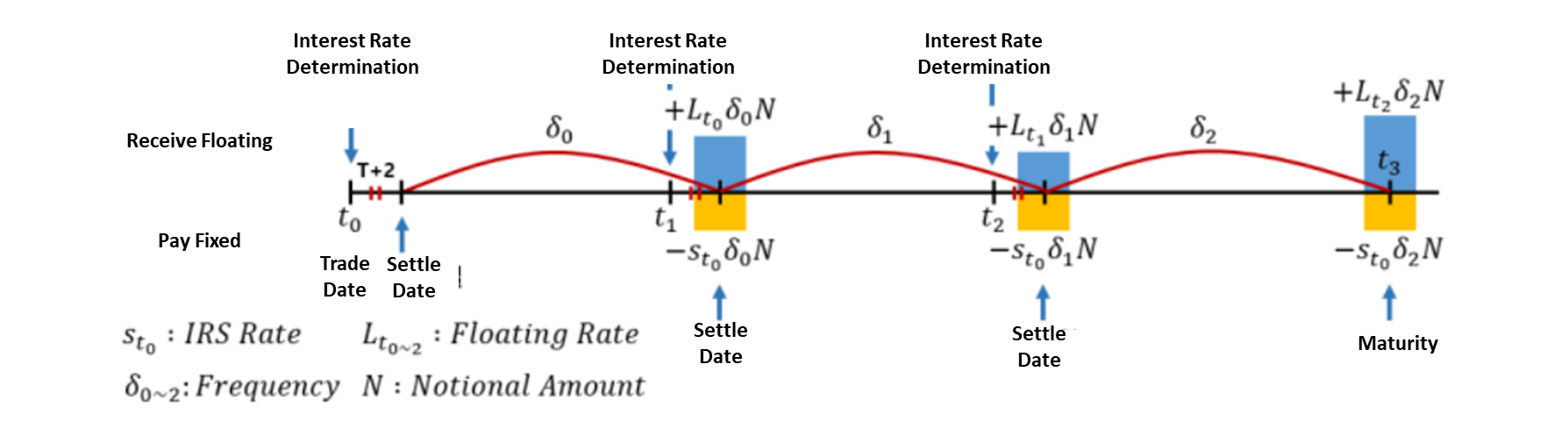
Seller of interest rate swap(IRS)
On contrary, If you think that interest rate will fall soon, you will sell IRS to counterparty. If rate falls as you expected, floating interest payment you need to pay to buyer will decrease.
How to understand IRS?
Of course, IRS might seems complicated to some of you. If you decompose IRS vertically, you can easily understand that IRS is simply sum of selling fixed interest rate bond and buying floating rate bond. So, you pay fixed and receive floating. This mitigates risk of interest rate rise. See picutre below.
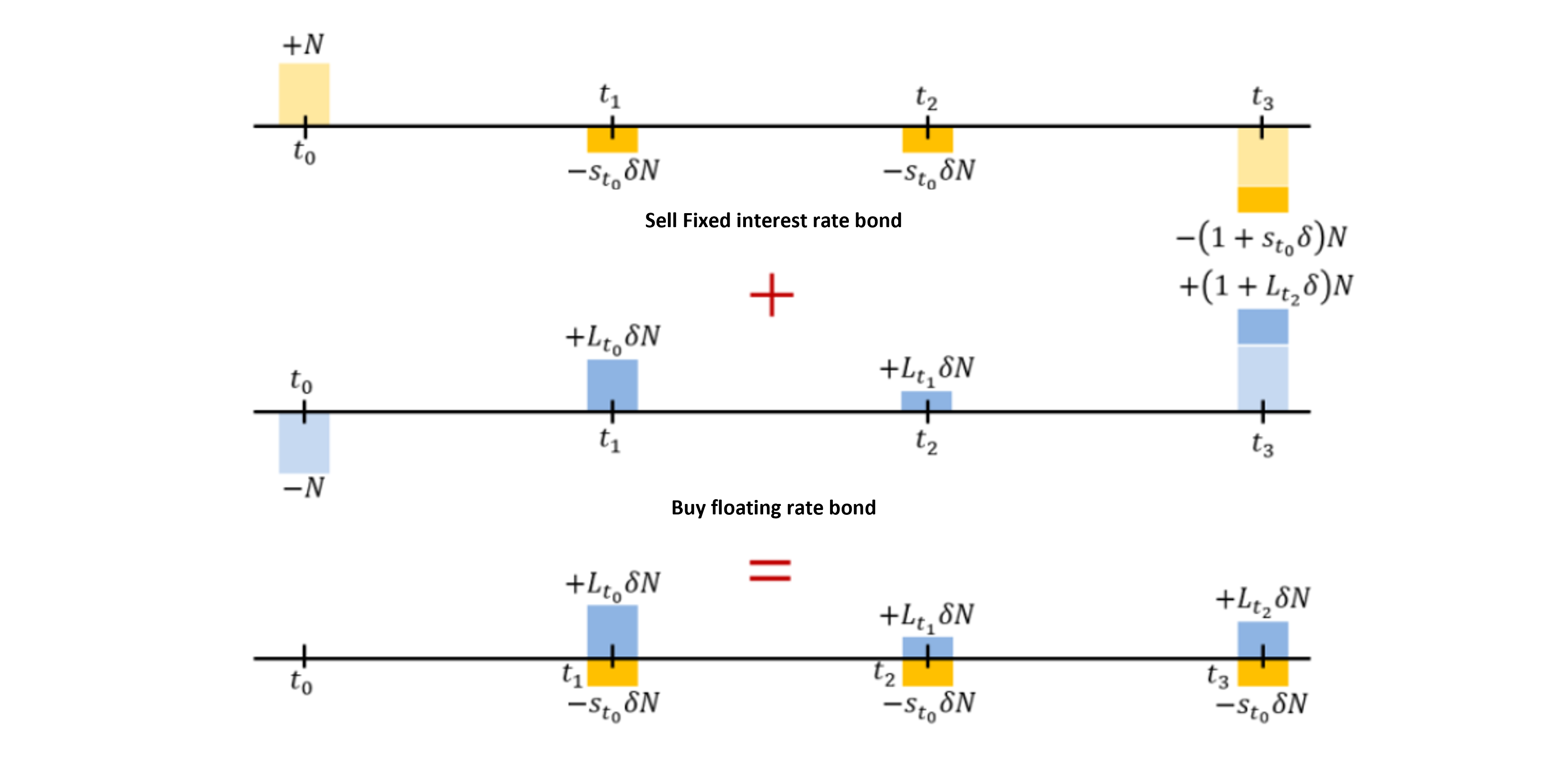
In addition, IRS can be expressed in horizontally. Cashflow of IRS is sum of combined forward rate aggrements. If we sum value of forward rate aggrement with different maturity, you can calculate value of IRS. See picture below. 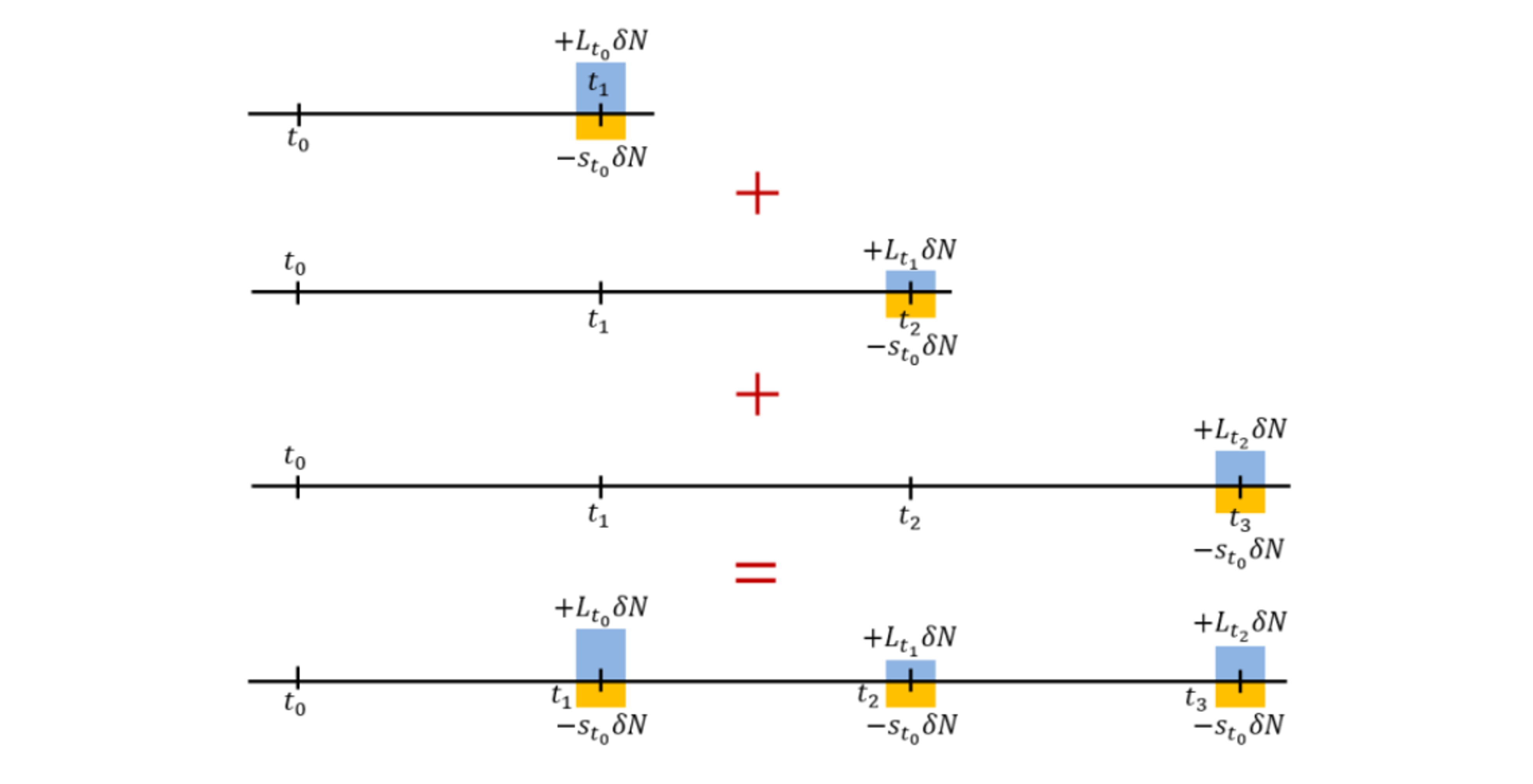
Summary
See below picture, if you are facing trouble in memorizing the IRS structure. 
Prequisite
1
from quant_lib.swap_curve import get_quote, swap_curve
If you don’t want to make your own swap curve library, go to this link and download and place it appripriate directory. Swap_Curve_Code Swap_Curve_Notebook
for example, let’s price IRS for buyers
1
2
3
4
5
6
7
8
9
10
11
issueDate = 10/9/2022
pricingDate = 1/9/2021
maturityDate = 4/9/2021
tenor = quarterly
swap rate = 2.18%
face value = 1000000
settlement days = first date of month
price of IRS = 16.134813731714075
delta of IRS = 25.262571390637277
theta of IRS = -2.3642255974538102
Let’s code this idea
Full code can be found at below link. CODE
Full Code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
import os
import datetime
import numpy as np
import pandas as pd
import QuantLib as ql
from quant_lib.swap_curve import get_quote, swap_curve
class IRS():
def __init__(self, today, pricing_date, maturity_date, irs_rate, notional, position, spread=0.0):
# initial setup
self.date = today
self.curve = self.CURVE(self.date)
self.pricing_date = ql.Date(pricing_date.day, pricing_date.month, pricing_date.year)
self.maturity_date = ql.Date(maturity_date.day, maturity_date.month, maturity_date.year)
self.calendar = ql.UnitedStates()
self.convention = ql.ModifiedPreceding
self.day_counter = ql.Actual360()
self.fixed_tenor = ql.Period(1, ql.Years)
self.float_tenor = ql.Period(3, ql.Months)
self.irs_rate = irs_rate
self.notional = notional
if position == 'long':
self.position = ql.VanillaSwap.Payer
else:
self.position = ql.VanillaSwap.Receiver
self.spread = spread
# pricing result
self.npv = self.PRICING(self.curve)
self.delta = self.DELTA()
self.theta = self.THETA()
def CURVE(self, date):
return swap_curve(date, get_quote(date))
def PRICING(self, curve):
#yield term structure
curve_handle = ql.YieldTermStructureHandle(curve)
# USD 3M Libor
float_index = ql.USDLibor(ql.Period(3, ql.Months), curve_handle)
# Fixed Schedule
fixedSchedule= ql.Schedule(self.pricing_date, # effectiveDate
self.maturity_date, # terminationDate
self.fixed_tenor, # tenor
self.calendar, # calendar
self.convention, # convention
self.convention, # terminationDateConvention
ql.DateGeneration.Backward, # rule
False # endOfMonth
)
# Fixed Schedule
floatingSchedule= ql.Schedule(self.pricing_date, # effectiveDate
self.maturity_date, # terminationDate
self.float_tenor, # tenor
self.calendar, # calendar
self.convention, # convention
self.convention, # terminationDateConvention
ql.DateGeneration.Backward, # rule
False # endOfMonth
)
# Interest Rate Swap
irs = ql.VanillaSwap(self.position,
self.notional,
fixedSchedule,
self.irs_rate,
self.day_counter,
floatingSchedule,
float_index,
self.spread,
self.day_counter
)
# pricing engine
swapEngine = ql.DiscountingSwapEngine(curve_handle)
irs.setPricingEngine(swapEngine)
# IRS pricing
npv = irs.NPV()
return npv
def DELTA(self):
# delta is change in values if 1bp of interest rate curve changes
# in here we use KRD (Key Rate Delta) not DV01
# KRD means how each tenor changes
curve_handle = ql.YieldTermStructureHandle(self.curve)
basis_point = 0.0001
# irs price when 1bp up
up_curve = ql.ZeroSpreadedTermStructure(
curve_handle,
ql.QuoteHandle(ql.SimpleQuote(basis_point))
)
up_irs = self.PRICING(up_curve)
down_curve = ql.ZeroSpreadedTermStructure(
curve_handle,
ql.QuoteHandle(ql.SimpleQuote(-basis_point))
)
down_irs = self.PRICING(down_curve)
#DV01
delta = (up_irs - down_irs)/2
return delta
def THETA(self):
# theta is change in value if one unit time passes.
# in here, unit time is 1 day
# since derivative product have time value, time to maturity is major variable in pricing derivatives
price_t0 = self.PRICING(self.CURVE(self.date))
price_t1 = self.PRICING(self.CURVE(self.date + datetime.timedelta(days=1)))
return price_t1 - price_t0
## set information
todays_date = datetime.date(2020, 10, 9)
pricing_date = datetime.date(2021, 1, 9)
maturity_date = datetime.date(2021, 4, 9)
position = 'long'
irs_rate = 0.00218
notional = 1000000
irs = IRS(
today=todays_date,
pricing_date=pricing_date,
maturity_date=maturity_date,
irs_rate=irs_rate,
notional=notional,
position=position,
spread=0.0
)
print("price of IRS = {}".format(irs.npv))
print("delta of IRS = {}".format(irs.delta))
print("theta of IRS = {}".format(irs.theta))