Money Weighted Return (Approximating with Taylor Series)

This post is about definition and approximation method for money weighted return (python code included)

What is Investment Return

When you invest, people might ask you how much you made profit, or how much return you made by the investment. There are single number for how much money you made, which can be expressed in dollars format. But to answer question how much profit(return) you recorded, you might be confused.
There are numerous ways to calculate investment return. These differ by how you tame time, cashflow during investment period, lookup time and so on. This post is about money weighted return. Another name of this method is IRR(Internal Rate of Return) which can be found in corporate finance field. Meaning that discount rate at which makes net present value of investment zero with out-cashflow $A_T$.

Definition of money weighted return

Let $0<t<T$ be time during investment and ${CF_t}$ be cash-flows on each date t. And let ${A_t}$ be cummulative investment amount at time t. Lastly, let $r_m$ be money weighted return from time $t=0$ and total money weighted return $R_m$.

(1) $ R_m = (1+r_m)^T - 1 $
(2) $ 0 = \sum_{t=0}^{T}\frac{CF_t}{(1+r_m)^t} - \frac{A_T}{(1+r_m)^T} $

multiplying $(1+r_m)^T$ on both side of equation givest polynomial equation.
(3) $ A_T = \sum_{t=0}^{T}CF_t (1+r_m)^{T-t} $

Since, $ T, CF_t, A_t $ are given as constant, unknown variable in above equation is $r_m$. But $(1+r_m)^{T-t}$ is n-th power form and thus makes it difficult to solve as T gets larger.
(4) $ (1+r_m)^(T-t) = {{T-t} \choose n} * r_m^n \fallingdotseq (2^n)(r_m^n) $

when $n \fallingdotseq \frac{1}{2}(T-t)$ and it may not be suppressed enough. Hence we have to keep all power of $r_m$ to the equation. But as power goes up, solving this equation requires huge computation. But if we replace $r_m$ to $R_m$ which is total money-weighted return over $0<t<T$, (2) can be written as below.
(5) $ A_t = \sum_{t=1}^{T}CF_t (1+R_m)^{(T-t)/T} $

Equation (5) is no longer polynomial equatiuon. but $\frac{T}{T-t} \in [0,1] $. Therefore, as long as $R_m$ is small, we can keep first few power of $R_m$ from the Taylor series of those therms.

Calculating money weighted return with python

Below code is

import numpy as np
import pandas as pd
from scipy.optimize import minimize
import yfinance as yf

# download S&P500 ETF data from yahoo
spy = yf.Ticker("SPY").history(period='1Y', start='2021-07-02')

# preprocessing time series data and return dataframe called 'asset'
# let's suppose that we are going to invest at beginning of month.
# investment period from 2021 July to 2022 June (1 year)
# During this period, severe market capitualtion were shown.

# money_weighted_return method is equation (5)
# calculate At with CF data and find solution of equation (5) in terms of R_m
def money_weighted_return(x,asset_df):
    formula = 0
    T = len(asset_df) -1
    for i in range(T):
        formula += asset_df.cf[i] * ((1 + x) ** ((T-i)/T))
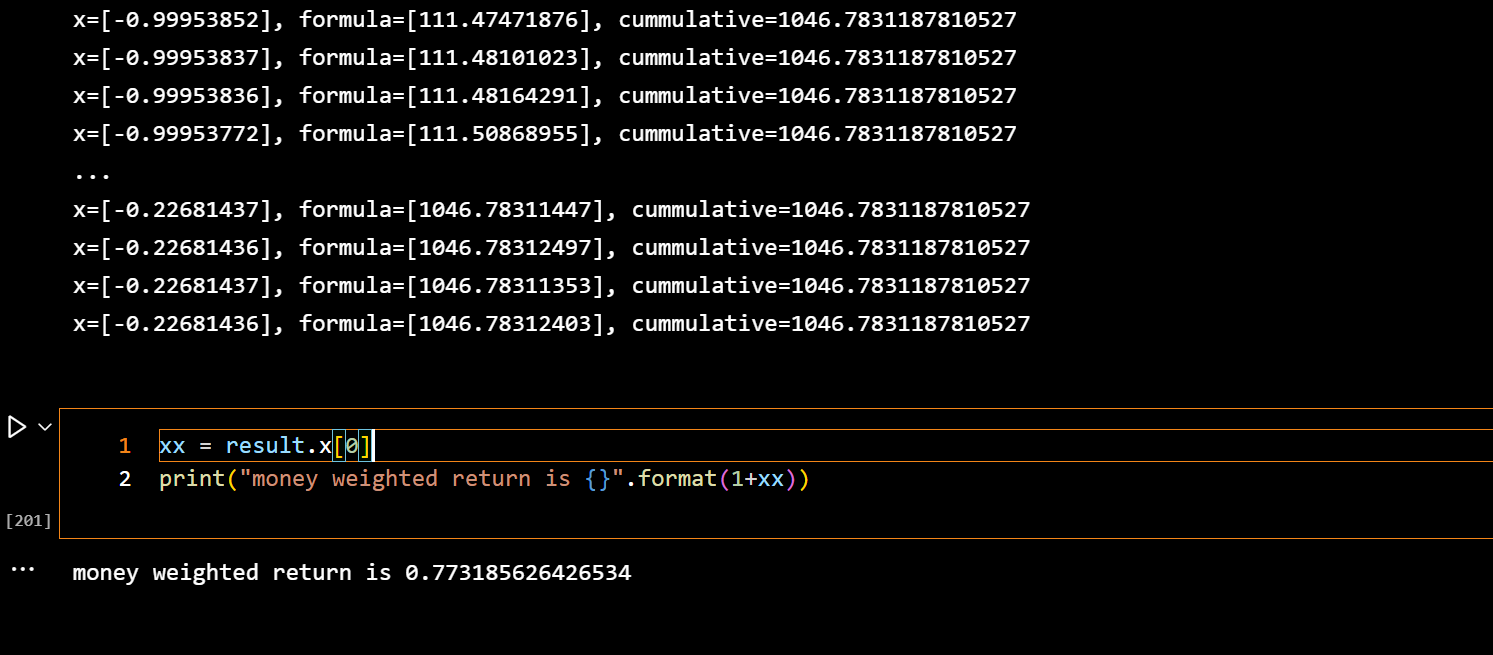
    print("x={}, formula={}, cummulative={}".format(x,formula, asset_df.cum[-1]))
    return abs(asset_df.cum[-1] - formula)

# use scipy minimize package 
result = minimize(fun = money_weighted_return,
                    args = (asset),
                    x0 = -1,
                    method = 'BFGS'
                    )

Comparing money weighted return with different returns

As shown cum column of asset dataframe, cumulative return (simple return) can be calculated by using account balance at last time and net cash inflow during investment horizon. 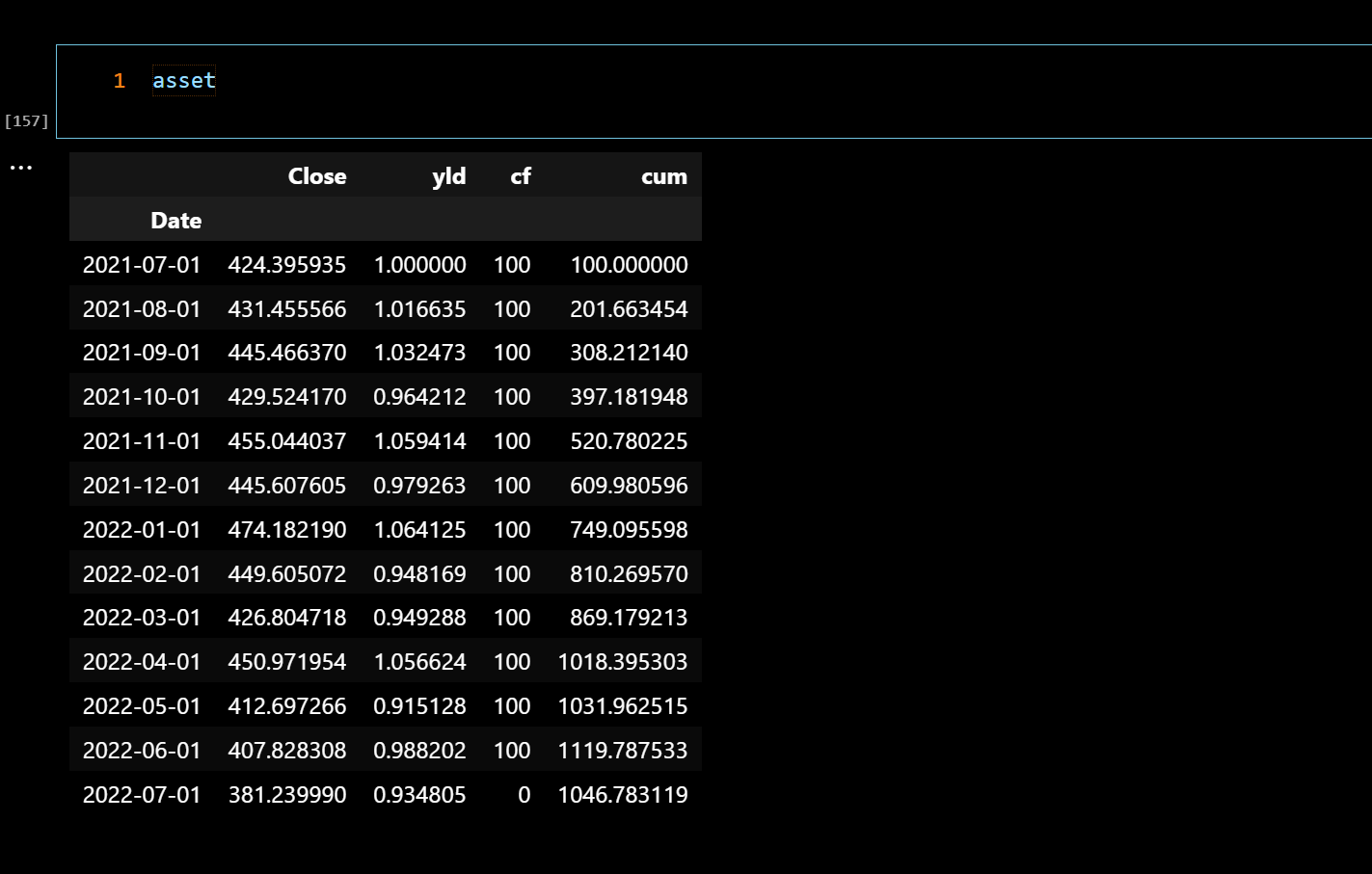Above asset dataframe is result of July 2021 to July 2022.

Proof