This post is about hierachical risk parity asset allocation strategy.
What is Hierachical Risk Parity strategy
Hierachical Risk Parity is revised version of risk parity strategy. It uses graph theory and unsupervised machine learning algorithm to build classical risk parity methods which allows better division of assets/factors into clusters with similar characteristics without relying on classical correlation analysis(pearson).
Hierachical Risk Parity algorithm cluster these asset classes according to some distance metric and then allocate equal risk budgets along these clusters. Such clusters might be deemed more natural building blocks than the aggregate risk factors in that they automatically pick up the dependence structure and form meaningful ingredients to aid portfolio diversitification.
How this works
First, hierarchical clustering algorithms uncover a hierarchical structure of the considered investment universe, resulting in a tree-based representation. Second, the portfolio weights result from applying an allocation strategy along the hierarchical structure and thus the overall portfolio is expected to exhibit a meaningful degree of diversification.
simple and short math
Given T x N matrix of stock return, and $\rho$ represent correlation matrix(N x N) of portfolio. And let converted correlation-distance matrix D and $\overline{D}$ as Eulidean distance between all the columns in pair-wise manner.
$ D(i, j) = \sqrt{0.5 * (1 – ⍴(i, j))} $
$ \overline{D}(i, j) = \sqrt{\sum_{k=1}^{N}(D(k, i) – D(k, j))^{2}} $
To summarize, $D(i, j)$ represents distance between two assets and $overline{D}(i, j)$ represents closeness in similarity of these assets with the rest of the portfolio.
Now let us denote set of cluster U. And below table is $\overline{D}$,
1
2
3
4
5
6
a b c d e
a 0 17 21 31 23
b 17 0 30 34 21
c 21 30 0 28 39
d 31 34 28 0 43
e 23 21 39 43 0
$ U[1] = argmin_{(i,j)} \overline{D}(i, j) $
(a,b) and (b,a) returns minimum distance thus combine these two into a cluster. And update matrix D
Updated matrix will be like
1
2
3
4
5
(a,b) c d e
(a,b) 0 21 31 23
c 21 0 28 39
d 31 28 0 43
e 21 39 43 0
$ \overline{D}(i, U[1]) = min( \overline{D}(i, a), \overline{D}(i, b))$
Go recursively combining assets into clusters
1
2
3
((a,b),c,e) d
((a,b),c,e) 0 28
d 28 0
$ \overline{D}(c, U[1]) = min( \overline{D}(c, a), \overline{D}(c, b) ) = min(21, 30) = 21 $
$ \overline{D}(d, U[1]) = min( \overline{D}(d, a), \overline{D}(d, b) ) = min(31, 34) = 31 $
$ \overline{D}(e, U[1]) = min( \overline{D}(e, a), \overline{D}(e, b) ) = min(23, 21) = 21 $
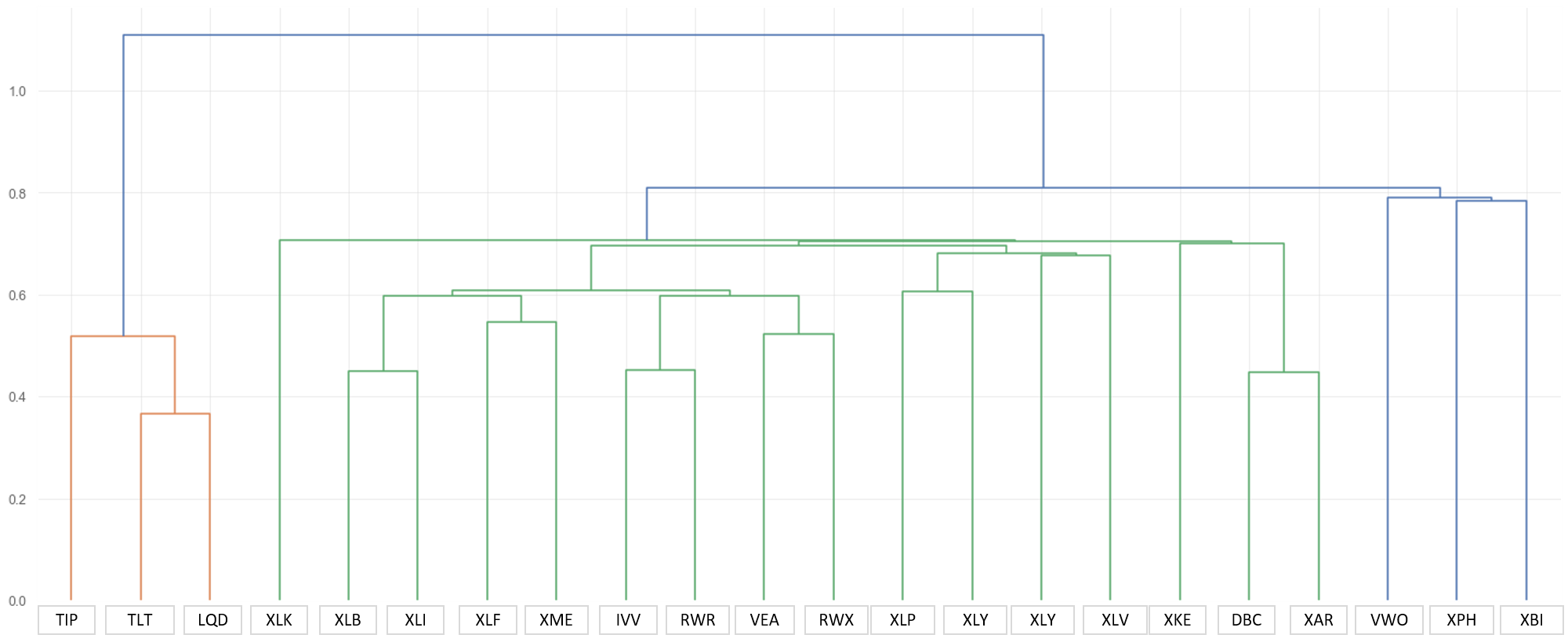
If we continue build this hierachy, result will be visualized as follows. This image is snap shot of investment universe. Hierachy structure chage dynamically at each year.
Data used (index)
I used index data from major index maker. All index are available in ETF(Exchange Traded Fund) form and can be traded easily.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
IVV : iShares Core S&P 500 ETF
VEA : Vanguard FTSE Developed Markets ETF
VWO : Vanguard FTSE Emerging Markets ETF
TLT : iShares
TIP : iShares TIPS Bond ETF
LQD : iShares iBoxx $ Investment Grade Corporate Bond ETF
DBC : Invesco DB Commodity Index Tracking Fund
XAR : SPDR® S&P® Aerospace & Defense ETF
XLB : The Materials Select Sector SPDR® Fund
XLE : The Energy Select Sector SPDR® Fund
XLF : The Financial Select Sector SPDR® Fund
XLI : The Industrial Select Sector SPDR® Fund
XLK : The Technology Select Sector SPDR® Fund
XME : SPDR® S&P® Metals & Mining ETF
XLP : The Consumer Staples Select Sector SPDR® Fund
XLY : The Consumer Discretionary Select Sector SPDR® Fund
XLU : The Utilities Select Sector SPDR® Fund
XLV : The Health Care Select Sector SPDR® Fund
XPH : SPDR® S&P® Pharmaceuticals ETF
XBI : SPDR® S&P® Biotech ETF
RWR : SPDR® Dow Jones® REIT ETF
RWX : SPDR® Dow Jones® International Real Estate ETF
Benchmark for this strategy is all weather porfolio of Ray Dalio.
1
2
3
4
5
Equity: MSCI All Country 30%
Long Fixed Income : Bloomberg US 20+ Treasury 40%
Mid-Short Fixed Income : Bloomberg US 7-10 Treasury 15%
Commodity : Gold Index 7.5%
Commodity : Goldmansachs Commodity Index 7.5%
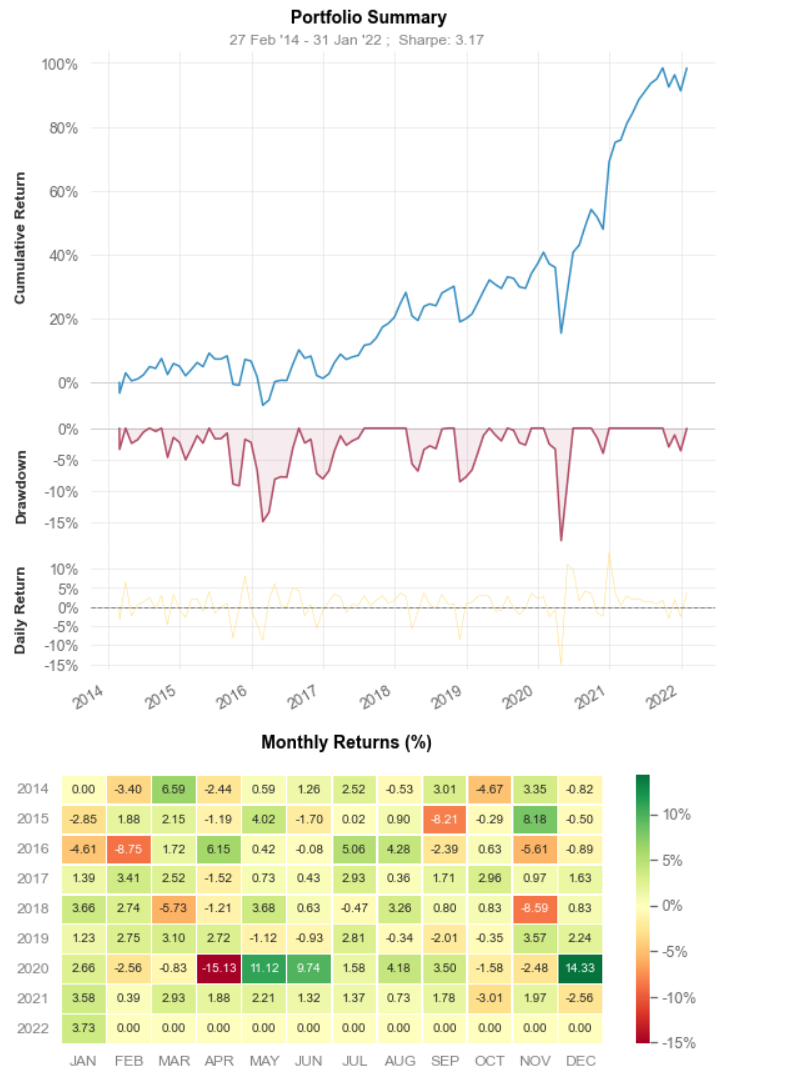
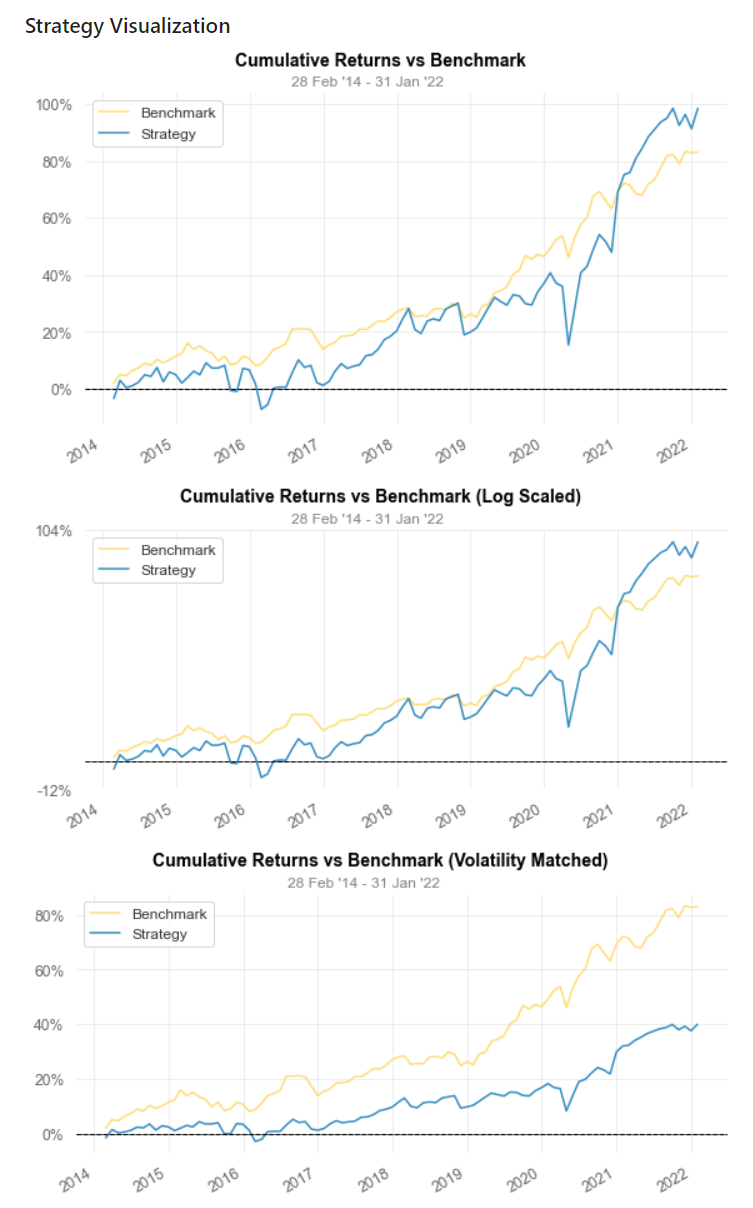
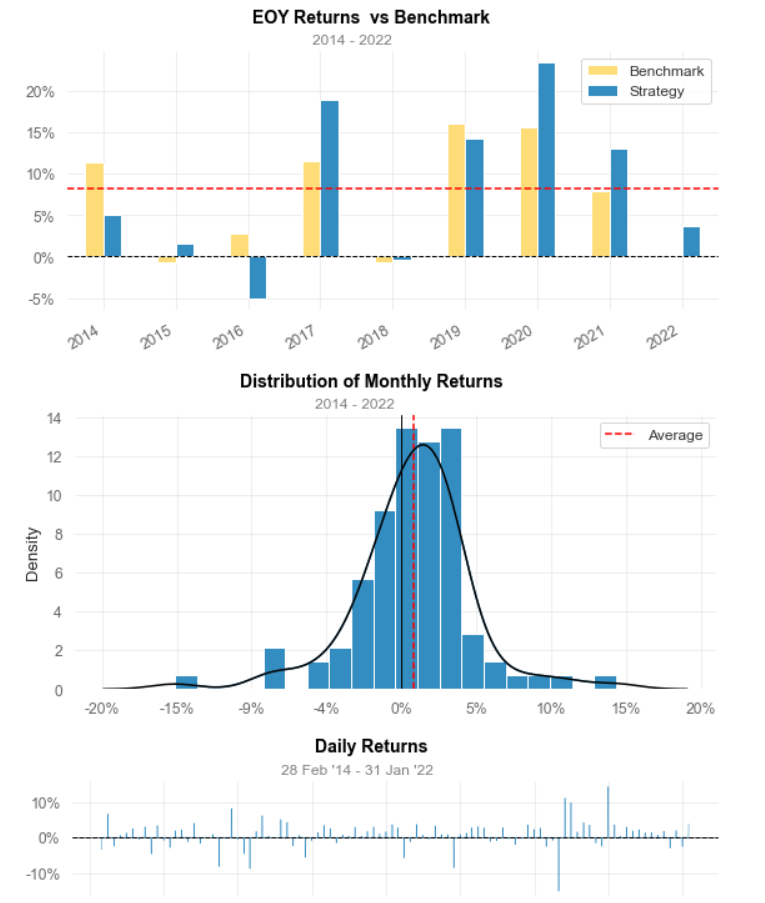
Strategy Overview
1
2
3
4
5
6
7
8
9
10
11
Strategy Benchmark
------------------ ---------- -----------
Start Period 2014-02-28 2014-02-28
End Period 2022-01-31 2022-01-31
Cumulative Return 98.37% 83.06%
CAGR﹪ 9.02% 7.92%
Sharpe 3.19 5.63
Expected Shortfall (cVaR) -5.71% -2.36%
Max Drawdown -17.99% -6.86%
Full Code
You can see full code in here CODE
Let’s code this idea
Hierachical Risk Parity via pyhton code.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
def hierachical_rp_portfolio(yld_df):
asset_cov = yld_df.cov()
asset_corr = yld_df.corr()
# distance matrix
d_corr = (np.sqrt(0.5*(1-asset_corr))).fillna(0)
link_corr = linkage(d_corr,'single')
z = pd.DataFrame(link_corr)
sort_index = get_quasi_diag(link_corr)
weights = get_rec_bipart(cov=asset_cov, sort_ix=sort_index)
weights.index = [yld_df.columns[i] for i in weights.index]
return weights
def get_quasi_diag(link):
# sort clustered items by distance
link = link.astype(int)
# get the first and the second item of the last tuple
sort_ix = pd.Series([link[-1,0], link[-1,1]])
# the total num of items is the third item of the last list
num_items = link[-1,3]
# if the max of sort_ix is bigger than or equal to the max_items
while sort_ix.max() >= num_items:
sort_ix.index = range(0, sort_ix.shape[0]*2, 2) # make space
df0 = sort_ix[sort_ix >= num_items] # find clusters
# df0 contains even index and cluster index
i = df0.index
j = df0.values - num_items
sort_ix[i] = link[j,0] # item 1
df0 = pd.Series(link[j, 1], index=i+1)
sort_ix = sort_ix.append(df0) # item 2
sort_ix = sort_ix.sort_index()
sort_ix.index = range(sort_ix.shape[0])
return sort_ix.tolist()
def get_cluster_var(cov, c_items):
cov_ = cov.iloc[c_items, c_items] # matrix slice
# calculate the inverse-variance portfolio
ivp = 1./np.diag(cov_)
ivp/=ivp.sum()
w_ = ivp.reshape(-1,1)
c_var = np.dot(np.dot(w_.T, cov_), w_)[0,0]
return c_var
def get_rec_bipart(cov, sort_ix):
# compute HRP allocation
# intialize weights of 1
w = pd.Series(1, index=sort_ix)
# intialize all items in one cluster
c_items = [sort_ix]
while len(c_items) > 0:
# bisection
c_items = [i[int(j):int(k)] for i in c_items for j,k in
((0,len(i)/2),(len(i)/2,len(i))) if len(i)>1]
# parse in pairs
for i in range(0, len(c_items), 2):
c_items0 = c_items[i] # cluster 1
c_items1 = c_items[i+1] # cluter 2
c_var0 = get_cluster_var(cov, c_items0)
c_var1 = get_cluster_var(cov, c_items1)
alpha = 1 - c_var0/(c_var0+c_var1)
w[c_items0] *= alpha
w[c_items1] *=1-alpha
return w
Full Result
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
Strategy Benchmark
------------------------- ---------- -----------
Start Period 2014-02-28 2014-02-28
End Period 2022-01-31 2022-01-31
Risk-Free Rate 0.0% 0.0%
Time in Market 100.0% 100.0%
Cumulative Return 98.37% 83.06%
CAGR﹪ 9.02% 7.92%
Sharpe 3.19 5.63
Smart Sharpe 3.04 5.37
Sortino 4.91 10.03
Smart Sortino 4.68 9.57
Sortino/√2 3.47 7.09
Smart Sortino/√2 3.31 6.76
Omega 1.77 1.77
Max Drawdown -17.99% -6.86%
Longest DD Days 428 488
Volatility (ann.) 62.75% 29.03%
R^2 0.4 0.4
Calmar 0.5 1.15
Skew -0.39 -0.29
Kurtosis 3.85 0.35
Expected Daily % 0.72% 0.63%
Expected Monthly % 0.72% 0.63%
Expected Yearly % 7.91% 6.95%
Kelly Criterion 17.33% 33.61%
Risk of Ruin 0.0% 0.0%
Daily Value-at-Risk -5.71% -2.36%
Expected Shortfall (cVaR) -5.71% -2.36%
Gain/Pain Ratio 0.77 1.44
Gain/Pain (1M) 0.77 1.44
Payoff Ratio 0.75 1.01
Profit Factor 1.77 2.44
Common Sense Ratio 1.96 3.23
CPC Index 0.86 1.64
Tail Ratio 1.11 1.32
Outlier Win Ratio 2.82 4.85
Outlier Loss Ratio 2.11 4.57
MTD 3.73% 0.19%
3M -0.03% 0.43%
6M 2.48% 3.14%
YTD 3.73% 0.19%
1Y 17.31% 8.12%
3Y (ann.) 18.28% 13.88%
5Y (ann.) 14.31% 9.8%
10Y (ann.) 9.02% 7.92%
All-time (ann.) 9.02% 7.92%
Best Day 14.33% 4.86%
Worst Day -15.13% -4.97%
Best Month 14.33% 4.86%
Worst Month -15.13% -4.97%
Best Year 23.4% 16.01%
Worst Year -5.07% -0.68%
Avg. Drawdown -6.41% -2.25%
Avg. Drawdown Days 152 106
Recovery Factor 5.47 12.1
Ulcer Index 0.04 0.02
Serenity Index 10.14 15.13
Avg. Up Month 3.02% 1.87%
Avg. Down Month -4.04% -1.86%
Win Days % 64.58% 66.67%
Win Month % 64.58% 66.67%
Win Quarter % 72.73% 78.79%
Win Year % 77.78% 77.78%
Beta 1.36 -
Alpha -0.23 -
Strategy Evaluation
To be updated …