This post is about mean variance strategy(modern portfolio theory). Unlike other post, this post includes visualization which helps you to understand theorm.
What is Modern Portfolio Theory
Modern Portfolio Theory (MPT) was designed by Harry Markowitz. Key idea of this theorm is that more diversification, less risk of investment. In addition to this simple idea, the Markowitz propose that you can find optimal points where you can maximize investment return given risk levels. So, by solving optimization problem, you can find optimal point where you can maximize return and reducing risk (maximum sharpe ratio point).
simple and short math
Consider portfolio of N assets. $(x_1,x_2,x_3,x_4, … ,x_N)$, where weight of assets $x_i$ is $w_i$, and standard deviation of the asset $x_i$ is $std_i$.
Let us note covariance matrix of the assets $X = (x_1, x_2, …, x_N)$ by $\sum$ and risk contribution of each asset as $\sigma_i$. Expected return of portfolio = $\sum w_i x_i$ and variance of portfolio = $\sum \frac{x_i - \hat{x_i}}{n-1}$.
If we solve mean variance strategy via optimization problem, it will be $ \max_w[w^t \mu - \frac{\lambda}{2} w^t \sum w] $
Solution for this problem is below :
$ w = (\lambda \sum)^{-1} \mu $
This means that to solve this equation, inverse of covariance matrix is needed. This is problematic since correlation among asset classes sensitively react to small changes in volatility of stock markets. In addition, expected returns of each asset classes are in area of guess and depends on historical data. Unfortunately historical data might not repeat again in future or it never repeat again. So, methodology which sensitively reacts to historical data might not be efficient in real world.
Alternative ways to overcome this problem are setting constraints and new algorithm called Hierachical Risk Parity. First, I set quite strict constraints to avoid from corner solution. All representative asset classes should be included in portfolio. And weights of these asset classes will be higher than 10%, lower than 40%. Also, I wrote post about hierachical risk parity. Please take a look.
visualize these mathematical formula
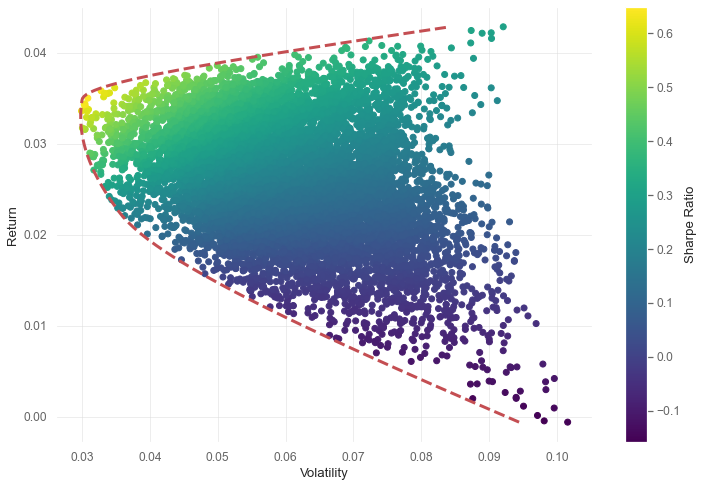
scatter plots means randomly generated portfolio using market index data. Red line means efficient frontier, represent best portfolio choice. This means that portfolio gave the highest return given risk level.
Data used and Benchmark for this strategy
I used index data from major index maker. Date from Jan 2006 to July 2022. All index are available in ETF(Exchange Traded Fund) form and can be traded easily. And benchmark for this strategy is 1/N portfolio.
1
2
3
4
5
6
7
US Equity Market : SPDR S&P 500 ETF Trust(SPY)
Developed Market : iShares MSCI EAFE ETF(EAF)
Emerging Market : iShares MSCI Emerging Markets ETF(EEM)
Short Term Bond : iShares 1-3 Year Treasury Bond ETF(SHY)
Long Term Bond : iShares 7-10 Year Treasury Bond ETF(IEF)
Ultra Long Term Bond : Shares 20+ Year Treasury Bond ETF (TLT)
IG Corporate Bond : iShares iBoxx Investment Grade Corporate Bond ETF(LQD)
Backtesting Detail
Monthly rebalancing is assumed. To calculate portfolio, I used monthly data to derive covariance matrix(lookup period = 1 month). Portfolio weight has sup/inf constraints which is (40%, 5%)
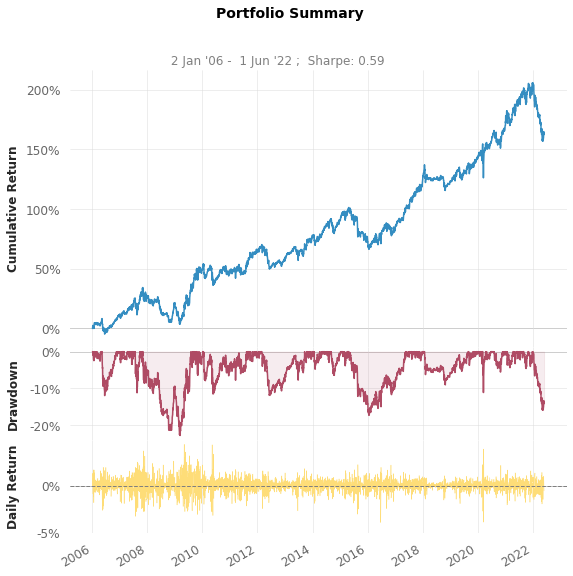
Strategy Overview
1
2
3
4
5
6
7
8
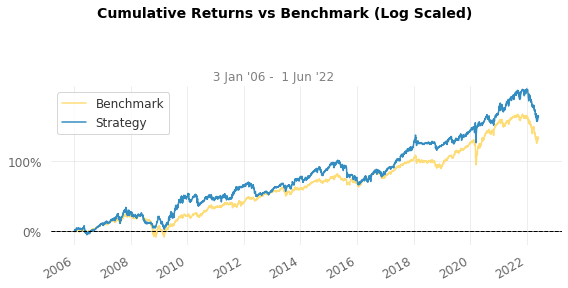
Strategy Benchmark
------------------------- ---------- -----------
Start Period 2006-01-03 2006-01-03
End Period 2022-06-01 2022-06-01
Cumulative Return 162.35% 131.9%
CAGR﹪ 6.05% 5.26%
Sharpe 0.59 0.6
Full Code
You can see full code in here CODE
Let’s code this idea
Mean variance strategy via python code.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
def generate_random_port():
num_ports = 10000
all_weights = np.zeros((num_ports, len(return_df.columns)))
ret, vol, sharpe = np.zeros(num_ports), np.zeros(num_ports), np.zeros(num_ports)
for x in range(num_ports):
# 4 means number of asset in universe.
# If you want to add more vehicle to universe, change this number
weights = np.array(np.random.random(4))
weights = weights/np.sum(weights)
return weights
def max_sharpe_portfolio(weight):
cons = (
{'type':'eq',
'fun':check_sum}
)
bounds = ((0,1),(0,1),(0,1),(0,1))
initial = [0.25, 0.25, 0.25, 0.25] # 1/N weight for default
optimizer = minimize(neg_sharpe, initial, method='SLSQP', bounds = bounds, constraints = cons)
print(optimizer)
print("Max Sharp portfolio consists of follows:")
print("{}% of dm stock".format(round(100*optimizer.x[0],2)))
print("{}% of em stock".format(round(100*optimizer.x[1],2)))
print("{}% of fixed income".format(round(100*optimizer.x[2],2)))
print("{}% of real estate".format(round(100*optimizer.x[3],2)))
return [
round(optimizer.x[0],2),
round(optimizer.x[1],2),
round(optimizer.x[2],2),
round(optimizer.x[3],2)
]
def get_ret_vol_sharpe(weight):
weight = np.array(weight)
ret = np.sum(return_df.mean() * weight) * 252
vol = np.sqrt(np.dot(weight.T, np.dot(return_df.cov()*252, weight)))
# set risk free rate as 1.5%
sharpe = (ret-0.015)/vol
return {'return':ret, 'volatility':vol, 'sharpe':sharpe}
def neg_sharpe(weight):
# to use convex optimization, change sign to minus to solve minimization problem.
return get_ret_vol_sharpe(weight)['sharpe'] * -1
# constraint : sum of weight should be less than equal to 1
def check_sum(weight):
#return 0 if sum of the weights is 1
return np.sum(weight)-1
Full Result
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
Strategy Benchmark
------------------------- ---------- -----------
Start Period 2006-01-03 2006-01-03
End Period 2022-06-01 2022-06-01
Cumulative Return 162.35% 131.9%
CAGR﹪ 6.05% 5.26%
Sharpe 0.59 0.6
Prob. Sharpe Ratio 99.09% 99.26%
Smart Sharpe 0.56 0.58
Sortino 0.83 0.86
Smart Sortino 0.79 0.82
Sortino/√2 0.58 0.61
Smart Sortino/√2 0.56 0.58
Omega 1.11 1.11
Max Drawdown -22.89% -26.37%
Longest DD Days 757 831
Volatility (ann.) 11.11% 9.21%
R^2 0.46 0.46
Information Ratio 0.01 0.01
Calmar 0.26 0.2
Skew -0.18 -0.01
Kurtosis 4.08 13.32
Expected Daily % 0.02% 0.02%
Expected Monthly % 0.49% 0.43%
Expected Yearly % 5.84% 5.07%
Kelly Criterion 3.04% 5.93%
Risk of Ruin 0.0% 0.0%
Daily Value-at-Risk -1.13% -0.93%
Expected Shortfall (cVaR) -1.13% -0.93%
Max Consecutive Wins 13 11
Max Consecutive Losses 10 10
Gain/Pain Ratio 0.11 0.12
Gain/Pain (1M) 0.68 0.75
Payoff Ratio 0.91 0.93
Profit Factor 1.11 1.12
Common Sense Ratio 1.07 1.07
CPC Index 0.54 0.57
Tail Ratio 0.96 0.95
Outlier Win Ratio 3.59 4.59
Outlier Loss Ratio 3.68 4.56
MTD -0.54% -0.58%
3M -8.64% -7.78%
6M -10.96% -11.25%
YTD -13.83% -12.23%
1Y -8.78% -10.22%
3Y (ann.) 4.57% 2.87%
5Y (ann.) 5.5% 3.95%
10Y (ann.) 5.38% 4.8%
All-time (ann.) 6.05% 5.26%
Beta 0.81 -
Alpha 0.02 -
Correlation 67.51% -
Treynor Ratio 199.36% -
Weight flow of portfolio over investment horizon 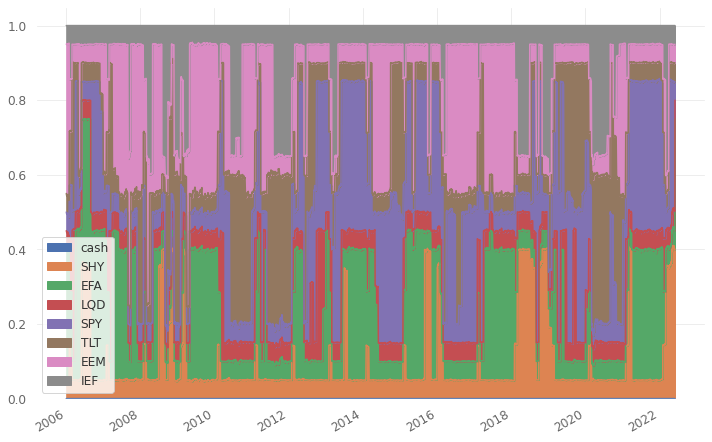
Distribution of the strategy and the benchmark 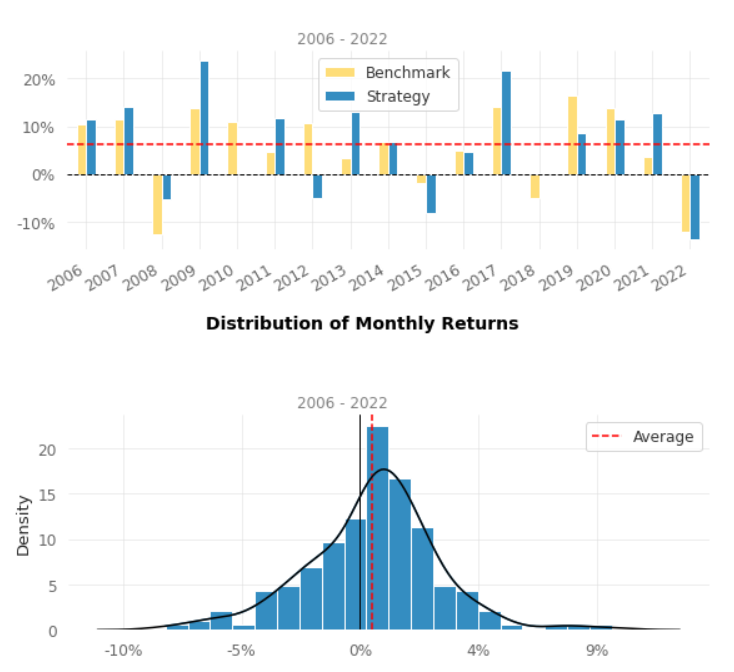
Monthly analysis of historical performance 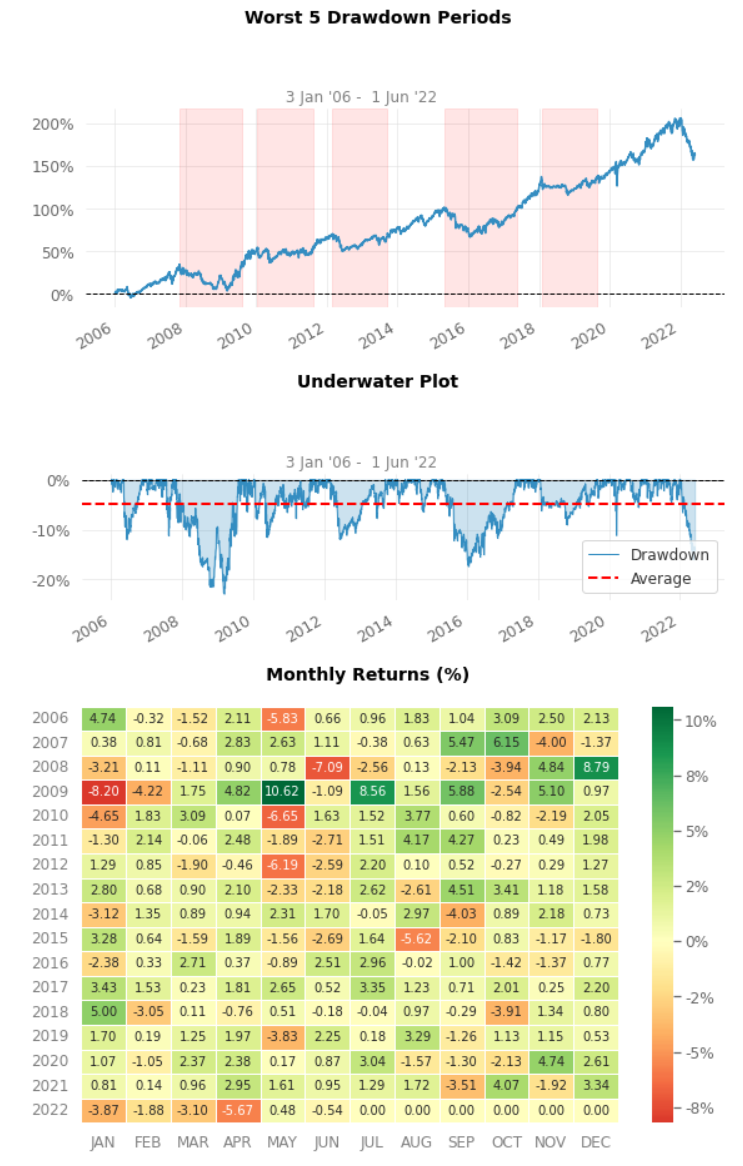
Strategy Evaluation
Evaluating investment strategy can be differ by investors and metrics. For high frequency trader, absoulte return is sole metric to evaluate the strategy. For long term investors, however other than absolute return should be considered. Such as risk, turnover, diversification ,,, and so on. Thus, less profitability doesn’t mean that the strategy is not good.
Markowitz Mean Variance Portfolio shows more stable investment return. However, investment returns heavily relies on return of equity. To sum up, fixed income investment portion offers stability to portfolio and equity investment offers profitability to portfolio.
But, optimizer itself showed better result than simple 1/N strategy in the aspect of returns. But sharpe ratio does not differ. So, careful consideration is required. Further calibration of parameter or constraints might enhance strategy such as lookup period, sup/inf constraints, turnover constraints. You can change parameter and find optimal solution.
Unfortunately, mean-variance optimization method itself is sensitive to historical return and risk. So, calibration might not guarantee robustness of strategy.