This post is about rate curve of treasury market. Data will be scaped from wsj site and quantlib library will be used.
What is Discount rate in finance?
One of the most important role of quant is to price financial products. In main street, cost which are shown in accounting report is one of the most important factor for pricing products they are selling. However, cost in financial product is ambigous. Recall finance 101, you might learned about Time Value of Money(TVM). TVM can be found at BA2-plus calculator. In here, we discount future cash flow, value to present value.
When we calculate PV, we multiply future CF with discount rate. Recall finance 101, when you calculate this, discount rate was given in your question. However, in real world what is that number? Answer to this question is interest rate which can be found at bond market. Just like stock market (NYSE, NASDAQ), bond markets are continous and make real-time number. You can use that number to price your financial product.
Why do we need curve?
Some might wonder, why we need curve instead of bond yield which can be shown at bloomberg terminal or yahoo finance. Answer to this question is the concept of “continous compounding”. Bond yield you can get from market is discret. Please click below link.
DATA
If you clik above url, you can go to Wall Street Journal market data page. Only bond yield you can get at bond tab are 1-month, 3-month, 6-month, 1-year, 2-years, 3-years, 5-years, 7-years, 10-years, 30-years.
If you want to price bond which has maturity of 12 years, what number you would use? Hmm…. Very difficult. You can clearly say 10-years, 30-years maturity bond yields. But 12 years maturity bond yield is difficult to answer. In here, the most optimal approach to this situation is approximation. Use piexewise informations, you can draw lines connecting dots and approximate 12 years maturity bond’s yield.
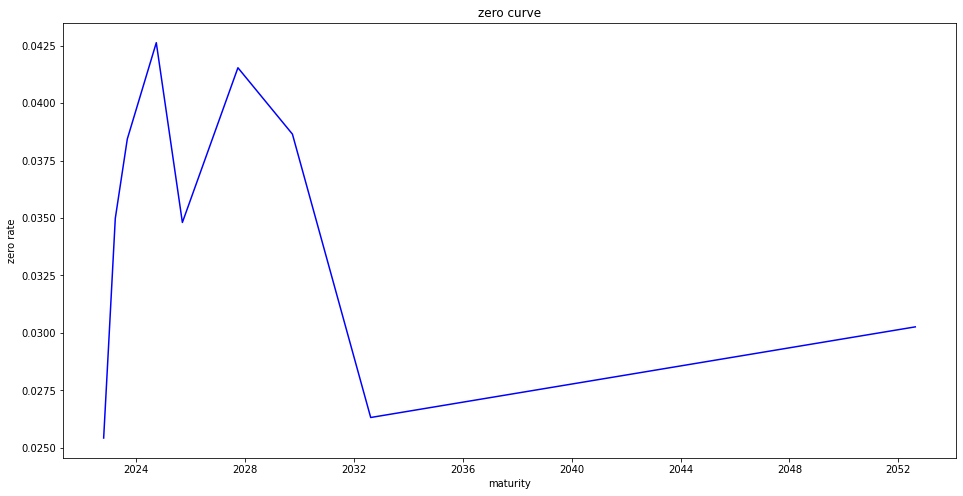
Inverted discount curve
Initial post is written at Oct, 2022. These days, yield curve is inverted. Interest rate for long maturity bond is lower than interest rate for short maturity bond. This phenomenon is uncommon. It only happens when macro economy is at severe recession and all people reluctant to invest money. So this can be signal for comming recession. If rate curve are back to normal, I will update this part.
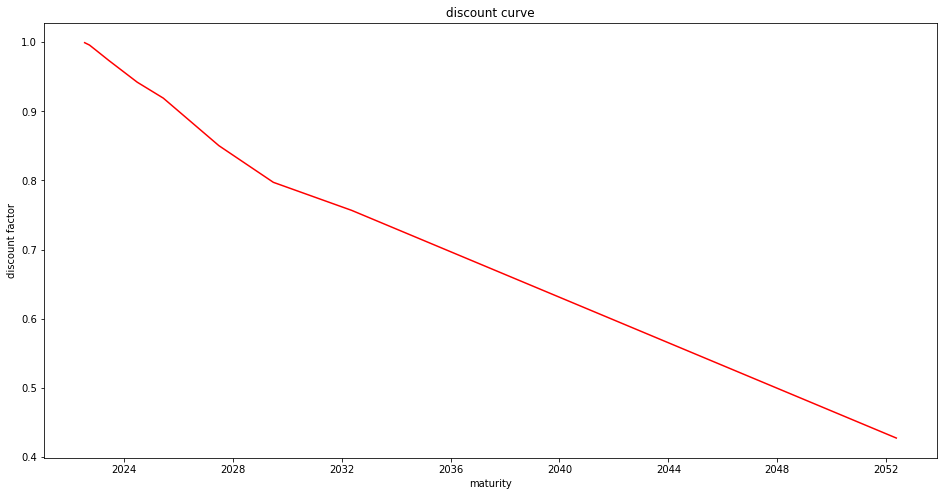
Result with real market data
1
2
3
4
5
6
7
8
9
10
11
12
days price coupon discount factor zero rate
maturity
2022-10-25 27 2.53 0.0 0.998133 0.025425
2022-12-29 92 3.301 0.0 0.992677 0.029375
2023-03-30 183 3.914 0.0 0.982763 0.034982
2023-09-07 344 3.803 0.0 0.964756 0.038435
2024-09-30 733 4.204 4.25 0.918859 0.042629
2025-09-15 1083 4.216 3.5 0.902767 0.034806
2027-09-30 1828 4.013 4.125 0.814004 0.041538
2029-09-30 2559 3.911 3.875 0.764772 0.038650
2032-08-15 3609 3.773 2.75 0.772329 0.026319
2052-08-15 10914 3.707 3.0 0.407590 0.030263
Getting bond data
You can get bond market data from Wall Street Journal. If you use python, you can use BeautifulSoup library to scrap data.
Scrap data from WSJ
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
import numpy as np
import pandas as pd
import datetime
import requests
from bs4 import BeautifulSoup
def get_quote(reference_date):
tenors = ['01M', '03M', '06M', '01Y', '02Y', '03Y','05Y','07Y','10Y','30Y']
# create empty lists
maturities = []
days = []
prices = []
coupons = []
headers = {'User-Agent': 'Mozilla/5.0'}
# get market informations
for i, tenor in enumerate(tenors):
url = "https://www.wsj.com/market-data/quotes/bond/BX/TMUBMUSD"+tenor+"?mod=md_bond_overview_quote"
req = requests.get(url, headers=headers)
html = req.text
soup = BeautifulSoup(html, 'html.parser')
# Price
data_src = soup.find("span", id="quote_val")
price = data_src.text
price = float(price[:-1])
data_src2 = soup.find_all("span", class_="data_data")
# Coupon
coupon = data_src2[2].text
if coupon != '':
coupon = float(coupon[:-1])
else:
coupon = 0.0
# Maturity Date
maturity = data_src2[3].text
maturity = datetime.datetime.strptime(maturity, '%m/%d/%y').date()
# Send to lists
days.append((maturity - reference_date).days)
prices.append(price)
coupons.append(coupon)
maturities.append(maturity)
# create dataframe
df = pd.DataFrame([maturities, days, prices, coupons]).transpose()
headers = ['maturity', 'days', 'price', 'coupon']
df.columns = headers
df.set_index('maturity', inplace=True)
return df
ref_date = get_date()
quote = get_quote(ref_date)
print(quote)
Let’s code this idea
Full code can be found at below link. CODE
Full Code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
def treasury_curve(date, quote):
# Divide Quotes
tbill = quote[0:4]
tbond = quote[4:]
# Set Evaluation Date
eval_date = ql.Date(date.day, date.month, date.year)
ql.Settings.instance().evaluationDate = eval_date
# Set Market Conventions
calendar = ql.UnitedStates()
convention = ql.ModifiedFollowing
day_counter = ql.ActualActual()
end_of_month = False
fixing_days = 1
face_amount = 100
coupon_frequency = ql.Period(ql.Semiannual)
# Construct Treasury Bill Helpers
bill_helpers = [ql.DepositRateHelper(ql.QuoteHandle(ql.SimpleQuote(r/100.0)),
ql.Period(m, ql.Days),
fixing_days,
calendar,
convention,
end_of_month,
day_counter)
for r, m in zip(tbill['price'], tbill['days'])]
# Construct Treasury Bond Helpers
bond_helpers = []
for p, c, m in zip(tbond['price'], tbond['coupon'], tbond['days']):
termination_date = eval_date + ql.Period(m, ql.Days)
schedule = ql.Schedule(eval_date,
termination_date,
coupon_frequency,
calendar,
convention,
convention,
ql.DateGeneration.Backward,
end_of_month)
bond_helper = ql.FixedRateBondHelper(ql.QuoteHandle(ql.SimpleQuote(100)),
fixing_days,
face_amount,
schedule,
[c/100.0],
day_counter,
convention)
bond_helpers.append(bond_helper)
# Bind Helpers
rate_helper = bill_helpers + bond_helpers
# Build Curve
yc_linearzero = ql.PiecewiseLinearZero(eval_date, rate_helper, day_counter)
return yc_linearzero
def discount_factor(date, curve):
# returns discount factors of each day
# use quantlib date type
print(date)
date = ql.Date(date.day, date.month, date.year)
return curve.discount(date)
def zero_rate(date, curve):
date = ql.Date(date.day, date.month, date.year)
day_counter = ql.ActualActual()
compounding = ql.Compounded
freq = ql.Continuous
zero_rate = curve.zeroRate(date, day_counter, compounding, freq).rate()
return zero_rate