This post is about application of Relative(Cross-Sectional) Momentum in Sector Rotation to financial investors.
What is Momentum
Momentum is concept used in physics field.
Momentum is defined as product of the mass of a particle and its velocity. Momentum is a vector quantity; i.e., it has both magnitude and direction. From Newton’s second law it follows that, if a constant force acts on a particle for a given time, the product of force and the time interval (the impulse) is equal to the change in the momentum. Conversely, the momentum of a particle is a measure of the time required for a constant force to bring it to rest. Definition of Momentum
In finance domain, momentum means price movement trend. Stock price literally do “work” by forces (probably by market participants). If forces act on stock price, it will move up or down. If stock price move(both with magnitude and quantity) by forces. So, Mid-term momentum means stock price movement trend for mid-term period and Long-term means stock price movement trend for long-term period. Direction can be either postive to negative.
What is Sector
Sector in stock market can easily be found in ETFs. In 1999, MSCI and S&P Dow Jones Indices developed the Global Industry Classification Standard (GICS), seeking to offer an efficient investment tool to capture the breadth, depth and evolution of industry sectors.
List of standard sectors are as follows.
1
2
3
4
5
6
7
8
9
10
11
Energy
Material
Industrial
Consumer Discrretionary
Consumer Staples
Health Care
Financials
Information Technology
Communication Services
Utilities
Real Estate
MSCI (Morgan Stanley Capital International) offers index for this sectors. These indexes are used as underlying index of ETFs.
Define Momentum for Sector Rotation
Rule is simple, calcuate momentum of sectors and pick top 5 sectors. Weight them equally to portfolio.
Stock Price (Y) At Time t = $ Y_t $
12 month Momentum = $ \frac{Y_t}{Y_t-12} - 1 $
6 month Momentum = $ \frac{Y_t}{Y_t-6} - 1 $
3 month Momentum = $ \frac{Y_t}{Y_t-3} - 1 $
1 month Momentum = $ \frac{Y_t}{Y_t-1} - 1 $
Universe = $ {X_1, X_2, … , X_n} $
12 Month Momentum Score Of Asset i = $ M_i $
Select 5 sectors with highest momentum score and assign equl weight.
Selected Sector = $ {x_1, x_2, x_3, x_4, x_5} $
Selected Weight = $ {w_1, w_2, w_3, w_4, w_5} $
$ W_i $ = 1/5
Data used (index)
I used index data from major index maker. All index are available in ETF(Exchange Traded Fund) form and can be traded easily.
1
2
3
4
5
6
7
8
9
10
11
12
XLB : The Materials Select Sector SPDR® Fund 1998-12-16
XLE : The Energy Select Sector SPDR® Fund 1998-12-22
XLF : The Financial Select Sector SPDR® Fund 1998-12-22
XLI : The Industrial Select Sector SPDR® Fund 1998-12-22
XLK : The Technology Select Sector SPDR® Fund 1998-12-22
XME : SPDR® S&P® Metals & Mining ETF 2006-06-23
XLP : The Consumer Staples Select Sector SPDR® Fund 1998-12-22
XLY : The Consumer Discretionary Select Sector SPDR® Fund 1998-12-22
XLU : The Utilities Select Sector SPDR® Fund 1998-12-22
XLV : The Health Care Select Sector SPDR® Fund 1998-12-22
XPH : SPDR® S&P® Pharmaceuticals ETF 2006-06-22
XBI : SPDR® S&P® Biotech ETF 2006-02-06
Benchmark for this strategy is Buy and Hold S&P500 index.
1
Equity: S&P500 100% buy and hold.
Disclaimer
Original Paper suggested strategy using 12 month momentum. But result was below expected. Author of paper used data from 1927 and published in 2010. In here I used data from 2008 where ETF based investing strategy became popular. So, there is strong possibility that alpha of this strategy decay as paper is published and more traders are available to approach sector market easily via ETFs.
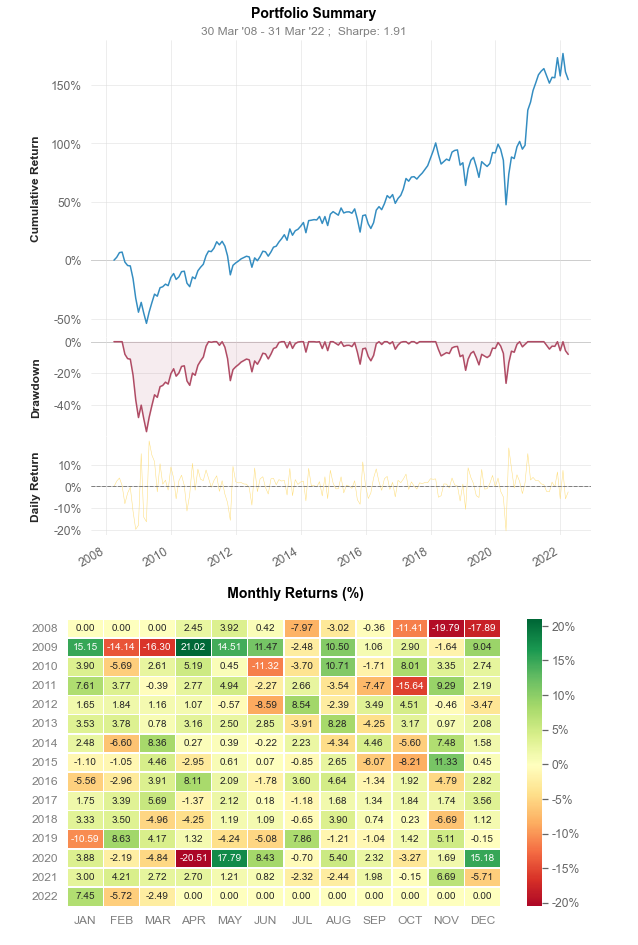
Strategy Overview _ 12 month momentum
1
2
3
4
5
6
7
8
9
10
11
Strategy Benchmark
------------------------- ---------- -----------
Start Period 2008-03-31 2008-03-31
End Period 2022-03-31 2022-03-31
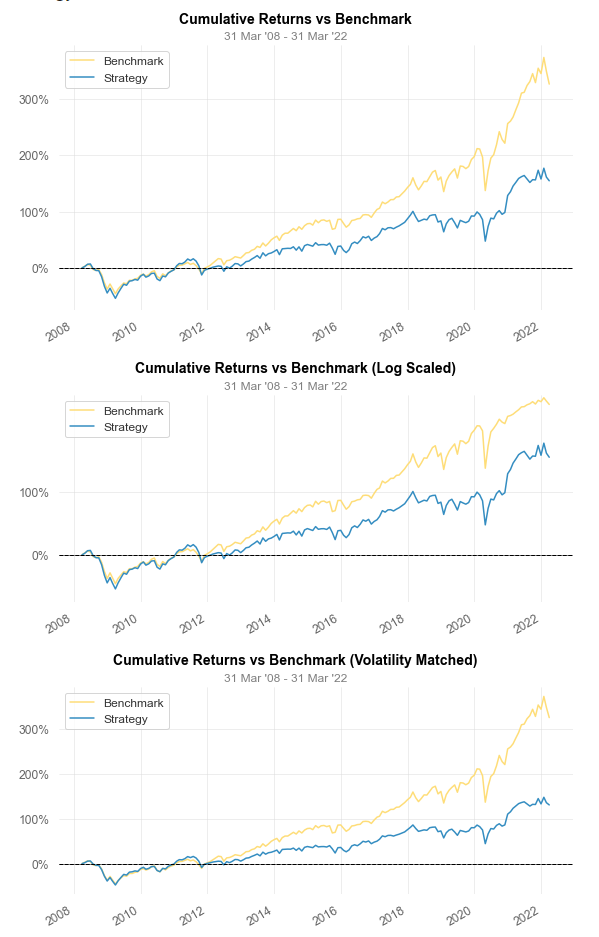
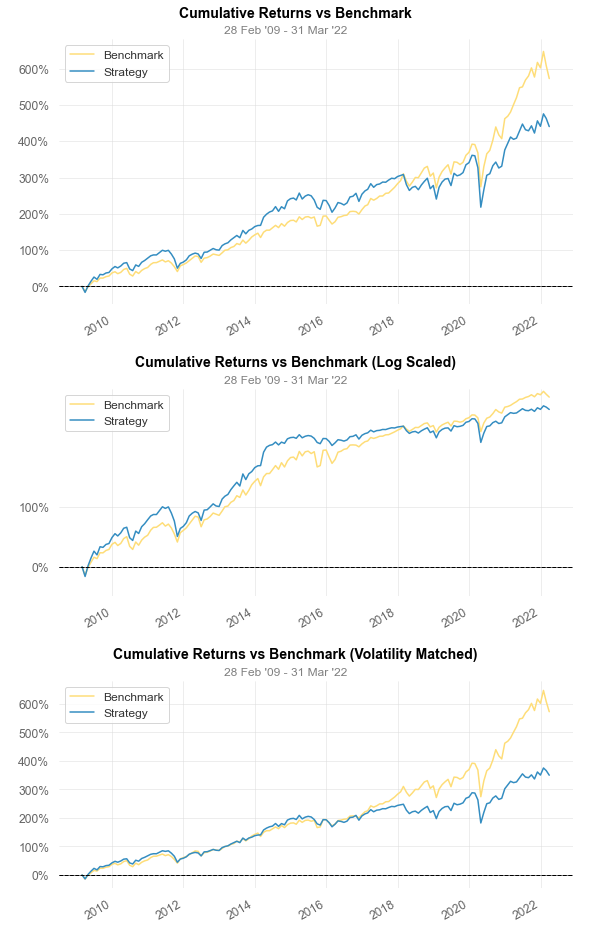
Cumulative Return 154.51% 326.02%
CAGR﹪ 6.9% 10.9%
Sharpe 1.92 3.01
Expected Shortfall (cVaR) -9.47% -7.69%
Max Drawdown -57.06% -48.93%
Full Code
You can see full code in here CODE
Let’s code this idea
Sector rotation with relative Momentum Criterion in multiple asset classes via python code.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
def get_momentum(yld_df):
"""
calculate momentum of sectors. use 12 month, 6 month, 3 month momentum to bit market
input
yiled_df : dataframe with weekly yield of asset classes
returns : momentum in pandas dataframe format. momentum of each asset classes for give date
"""
momentum = pd.DataFrame(columns = yld_df.columns, index = yld_df.index)
for asset in yld_df.columns:
i = 0
for date in yld_df.index:
# 52 weeks per year = 12 month
if i > windows :
# first 12 month data (52 data points) cannot be used since 12 month lagged returns is required
momentum.loc[date, asset] = yld_df[asset].iloc[i] / yld_df[asset].iloc[i - windows] - 1
else:
momentum.loc[date, asset] = 0
i = i + 1
momentum = momentum.replace([np.inf], 1000)
momentum = momentum.replace([-np.inf], -1000)
momentum = momentum.replace([np.nan], 0)
return momentum
def select_sector(yld_df):
"""
select top 5 sectors with highest momentum score
returns: selected_tickers in list format. list with top 5 momentum in given period`
"""
# inherit previous method and run
momentum_df = get_momentum(yld_df)
selected_momentum = pd.DataFrame(
columns=['momentum_1','momentum_2','momentum_3','momentum_4','momentum_5'],
index=momentum_df.index
)
selected_ticker = pd.DataFrame(
columns=['momentum_1','momentum_2','momentum_3','momentum_4','momentum_5'],
index=momentum_df.index
)
for date in momentum_df.index:
sorted_momentum = momentum_df.loc[date].sort_values(ascending=False)
for i in range(len(selected_momentum.columns)):
selected_momentum.loc[date,f'momentum_{i+1}'] = sorted_momentum[i]
selected_ticker.loc[date,f'momentum_{i+1}'] = sorted_momentum.index[i]
return selected_ticker
def sector_momentum(yld_df):
"""
returns : market portfolio in pandas dataframe format.
"""
# inherit previous method and run
# select_sector method returns tickers
mom_ticker_df = select_sector(yld_df)
mp_table = pd.DataFrame(columns=yld_df.columns, index=yld_df.index)
for date in yld_df.index:
selected = mom_ticker_df.loc[date].tolist()
for sel in selected:
mp_table.loc[date, sel] = 1/5
mp_table = mp_table.fillna(0)
return mp_table
def trim_data(yld_df, mp_table, benchmark_yield_df):
"""
since momentum strategy uses 12 month lagged momentum, first 12 month data cannot be used
return : yld_df, mp_table, bm_yld in dataframe format
"""
yld_df = yld_df.iloc[windows + 1:]
mp_table = mp_table.iloc[windows + 1:]
benchmark_yield_df = benchmark_yield_df.iloc[windows + 1:]
return yld_df, mp_table, benchmark_yield_df
Full Result
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
Strategy Benchmark
------------------------- ---------- -----------
Start Period 2008-03-31 2008-03-31
End Period 2022-03-31 2022-03-31
Risk-Free Rate 0.0% 0.0%
Time in Market 100.0% 100.0%
Cumulative Return 154.51% 326.02%
CAGR﹪ 6.9% 10.9%
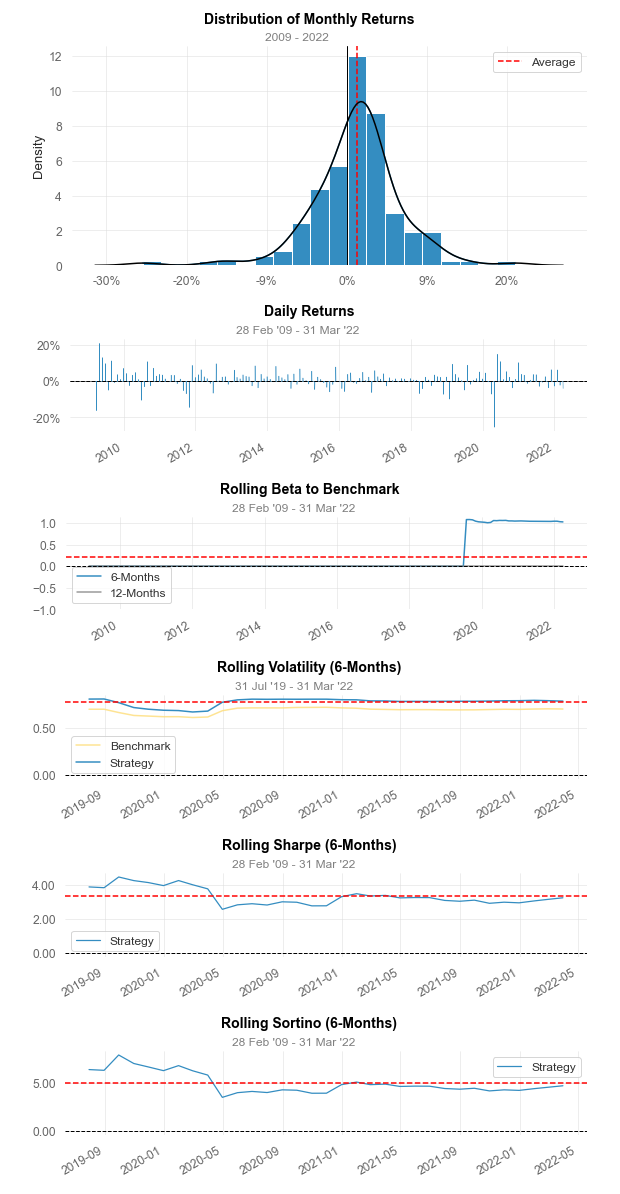
Sharpe 1.92 3.01
Smart Sharpe 1.88 2.97
Sortino 2.79 4.37
Smart Sortino 2.74 4.29
Sortino/√2 1.97 3.09
Smart Sortino/√2 1.94 3.04
Omega 1.4 1.4
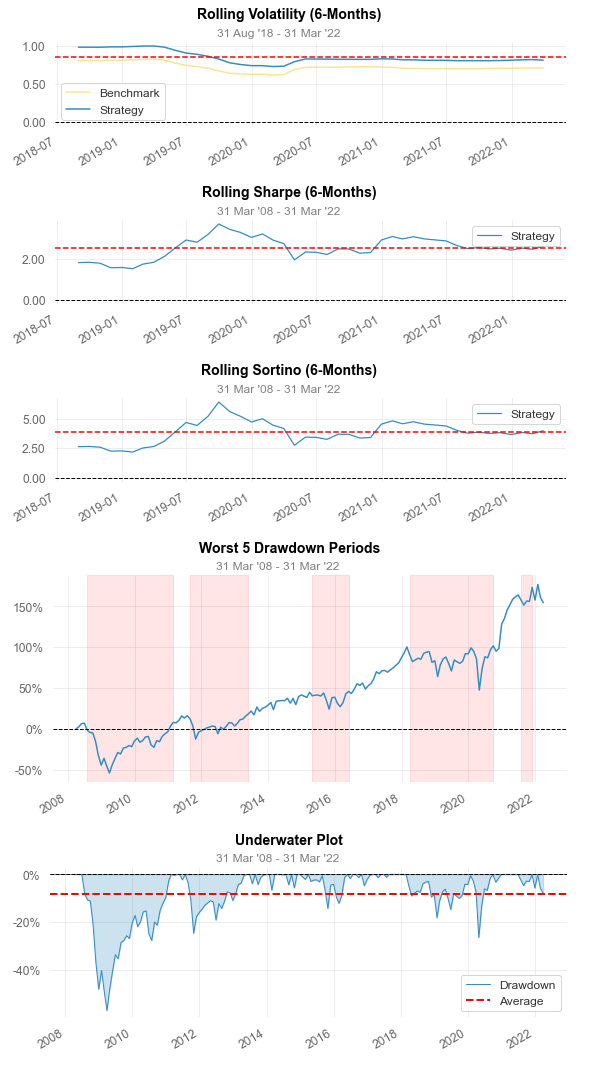
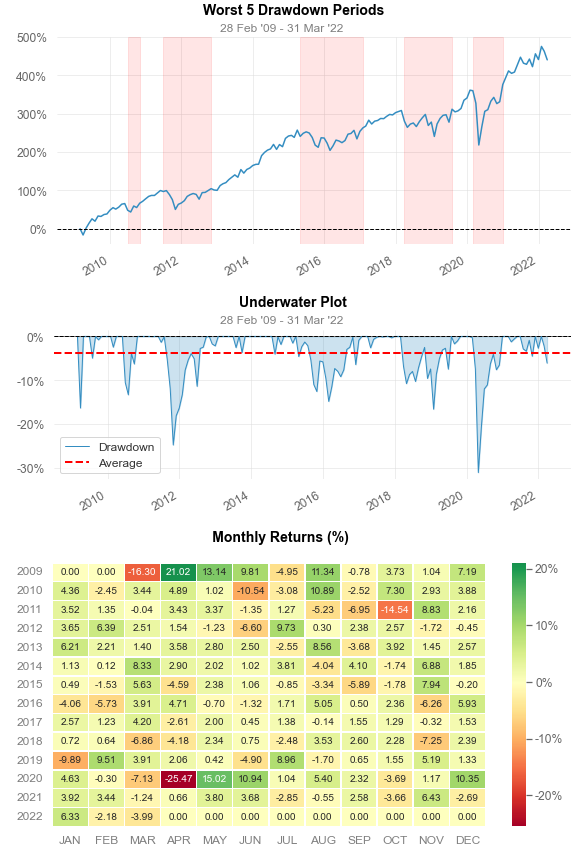
Max Drawdown -57.06% -48.93%
Longest DD Days 942 1034
Volatility (ann.) 98.65% 83.87%
R^2 0.89 0.89
Calmar 0.12 0.22
Skew -0.41 -0.78
Kurtosis 2.27 2.49
Expected Daily % 0.55% 0.86%
Expected Monthly % 0.55% 0.86%
Expected Yearly % 6.43% 10.14%
Kelly Criterion 10.85% 28.63%
Risk of Ruin 0.0% 0.0%
Daily Value-at-Risk -9.47% -7.69%
Expected Shortfall (cVaR) -9.47% -7.69%
Gain/Pain Ratio 0.4 0.67
Gain/Pain (1M) 0.4 0.67
Payoff Ratio 0.75 0.79
Profit Factor 1.4 1.67
Common Sense Ratio 1.43 1.59
CPC Index 0.65 0.9
Tail Ratio 1.02 0.95
Outlier Win Ratio 3.62 4.17
Outlier Loss Ratio 3.45 3.55
MTD -2.49% -5.05%
3M -6.85% -6.2%
6M 1.2% -1.04%
YTD -1.21% -4.2%
1Y 3.83% 15.91%
3Y (ann.) 11.43% 17.83%
5Y (ann.) 8.56% 14.72%
10Y (ann.) 9.62% 14.35%
All-time (ann.) 6.9% 10.9%
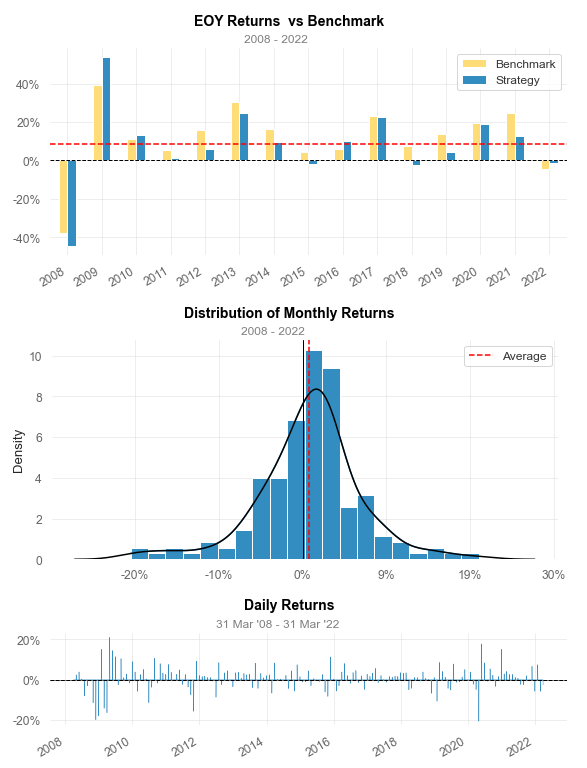
Best Day 21.02% 15.58%
Worst Day -20.51% -19.99%
Best Month 21.02% 15.58%
Worst Month -20.51% -19.99%
Best Year 53.65% 39.07%
Worst Year -44.52% -37.52%
Avg. Drawdown -8.57% -8.06%
Avg. Drawdown Days 178 123
Recovery Factor 2.71 6.66
Ulcer Index 0.14 0.11
Serenity Index 2.58 6.89
Avg. Up Month 4.37% 4.04%
Avg. Down Month -5.86% -5.1%
Win Days % 61.9% 68.45%
Win Month % 61.9% 68.45%
Win Quarter % 67.86% 76.79%
Win Year % 73.33% 86.67%
Beta 1.11 -
Alpha -0.92 -
Further Issue –> Alpha?
This strategy is published in 2010. Critical point here is that the author tested this strategy with data from 1970~. This means that alpha decay is most likely to occurs. Furthermore, as shown above, sector-theme based ETF get polular from 2015 ~.You can see significant underperformance from 2018. It’s not sure but it is likely that this strategy’s alpha got decayed by numerous traders in market. I tested this strategy with 3 month momentum, and this showed better result than 12 month momentum but still lower than benchmark index (S&P500 index)
Strategy Evaluation
To be updated …